Ángulo suma
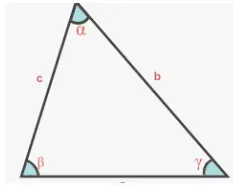
Según la propiedad de la suma de ángulos de un triángulo, la suma de los tres ángulos interiores de un triángulo es de 180 grados. Un triángulo es una figura cerrada formada por tres segmentos de línea, con ángulos interiores y exteriores. La propiedad de la suma de ángulos se usa para encontrar la medida de un ángulo interior desconocido cuando se conocen los valores de los otros dos ángulos.
Fórmula de la propiedad de la suma de ángulos
La fórmula de la propiedad de la suma de ángulos para cualquier polígono se expresa como, S = (n - 2) × 180°, donde 'n' representa el número de lados del polígono. Esta propiedad de un polígono establece que la suma de los ángulos interiores de un polígono se puede encontrar con la ayuda del número de triángulos que se pueden formar en su interior. Estos triángulos se forman trazando diagonales desde un solo vértice. Sin embargo, para facilitar las cosas, esto se puede calcular mediante una sencilla fórmula, que dice que si un polígono tiene "n" lados, habrá (n - 2) triángulos en su interior. Por ejemplo, tomemos un decágono que tiene 10 lados y apliquemos la fórmula. Obtenemos, S = (n - 2) × 180°, S = (10 - 2) × 180° = 10 × 180° = 1800°. Por tanto, según la propiedad de la suma de ángulos de un decágono, la suma de sus ángulos interiores es siempre 1800°. La misma fórmula puede aplicarse a otros polígonos. La propiedad de la suma de ángulos se utiliza sobre todo para encontrar los ángulos desconocidos de un polígono.
Prueba de la propiedad de la suma de ángulos
Los pasos para demostrar la propiedad de la suma de ángulos de un triángulo se indican a continuación:
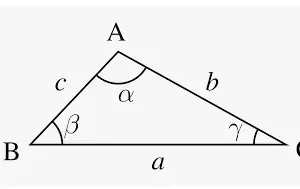
Paso 1: Dibuja una recta PQ que pase por el vértice A y sea paralela al lado BC del triángulo ABC.
Paso 2: Sabemos que la suma de los ángulos de una recta es igual a 180°. Es decir, ∠PAB + ∠BAC + ∠QAC = 180°, lo que da, la ecuación 1: ∠PAB + ∠BAC + ∠QAC = 180°.
Paso 3: Ahora, como la línea PQ es paralela a BC. ∠PAB = ∠ABC y ∠QAC = ∠ACB. (Ángulos alternos interiores), lo que da, la ecuación 2: ∠PAB = ∠ABC, y la ecuación 3: ∠QAC = ∠ACB.
Paso 4: Sustituir ∠PAB y ∠QAC por ∠ABC y ∠ACB respectivamente, en la Ecuación 1 como se muestra a continuación.
Ecuación 1: ∠PAB + ∠BAC + ∠QAC = 180°. Así obtenemos, ∠ABC + ∠BAC + ∠ACB = 180°.
Puntos importantes
Al resolver las preguntas relacionadas con la propiedad de la suma de ángulos se deben recordar los siguientes puntos.
- La fórmula de la propiedad de la suma de ángulos para cualquier polígono se expresa como, S = ( n - 2) × 180°, donde "n" representa el número de lados del polígono.
- La propiedad de la suma de ángulos de un polígono establece que la suma de los ángulos interiores de un polígono se puede encontrar con la ayuda del número de triángulos que se pueden formar en su interior.
- La suma de los ángulos interiores de un triángulo es siempre 180°.