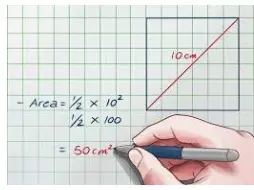
Centro de gravedad de un triángulo

El centroide de un triángulo es el punto a través del cual parece actuar toda la masa de una placa triangular. También se conoce como su "centro de gravedad", "centro de masa" o baricentro.

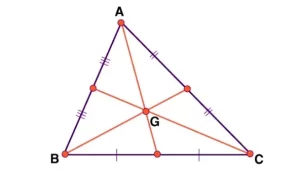
Un hecho fascinante es que el centroide es el punto de intersección de las medianas del triángulo.

• El centroide está siempre dentro del triángulo
• Cada mediana divide el triángulo en dos triángulos más pequeños de igual área.
• El centroide está exactamente a dos tercios de cada mediana.
• Dicho de otro modo, el centroide divide cada mediana en dos segmentos cuyas longitudes están en la proporción 2:1, siendo la más larga la más cercana al vértice. Estas longitudes se muestran en una de las medianas de la figura de la parte superior de la página para que puedas comprobar esta propiedad por ti mismo.

Centroide de un triángulo

En matemáticas, el centroide define el centro geométrico de una superficie plana bidimensional. Es un punto que se sitúa a partir de la posición media aritmética de todos los puntos de la superficie plana. En caso contrario, se define como la media de todos los puntos de la figura plana. El centroide se puede encontrar para diferentes formas geométricas.

Para una forma bidimensional "triángulo", el centroide se obtiene por la intersección de sus medianas. Los segmentos de línea de las medianas unen el vértice con el punto medio del lado opuesto. Las tres medianas se encuentran en un único punto (concurrente). El punto de concurrencia se conoce como el centroide de un triángulo.

En la figura dada, tres medianas de un triángulo se encuentran en un centroide "G". El centroide también se conoce como centro de gravedad.

Propiedades del centroide de un triángulo

Las propiedades importantes del centroide de un triángulo son:

• El centroide de un triángulo se encuentra en el punto de intersección de las tres medianas de un triángulo
• Se considera uno de los tres puntos de concurrencia de un triángulo, es decir, incentro, circuncentro y centroide
• El centroide se sitúa en el interior de un triángulo
• En el punto de intersección (centroide), cada mediana de un triángulo se divide en la proporción de 2: 1

Fórmula del centroide de un triángulo

Si las coordenadas de los vértices de un triángulo son (x1, y1), (x2, y2), (x3, y3), la fórmula del centroide del triángulo es la siguiente

El centroide de un triángulo = ((x1+x2+x3)/3, (y1+y2+y3)/3)

Donde,

x1, x2, x3 son las coordenadas x de los vértices de un triángulo.

y1, y2, y3 son las coordenadas y de los vértices de un triángulo.

Vídeos de Centro de gravedad de un triángulo