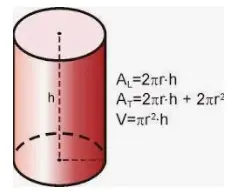
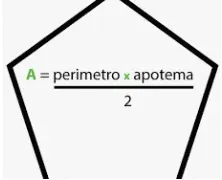
Ley del paralelogramo

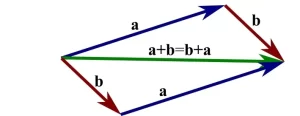
La ley del paralelogramo es una fórmula que relaciona los lados de un paralelogramo con sus diagonales. A grandes rasgos, la suma de los cuadrados de los lados del paralelogramo es igual a la suma de los cuadrados de las diagonales.

La Ley del Paralelogramo juega un papel fundamental en las matemáticas superiores. En un espacio vectorial dotado de un producto escalar u.v, la norma ||-| que se define como ||u||2 = u.u, satisface la Ley del Paralelogramo:

(1) ||u - v||2 + ||u + v||2 = 2(||u||2 + ||v||2)

La importancia de la ley proviene del hecho de que cualquier norma que satisfaga (1) está obligada a haberse originado a partir de un producto escalar. Por ejemplo, en un espacio vectorial real, el producto escalar puede definirse como

u.v = (||u + v||2 - ||u - v||2)/4, o
u.v = (|u + v||2 - |u||2 - |v||2)/2.

El producto real definido para dos números complejos es simplemente el producto escalar común de dos vectores. En geometría plana, la interpretación de la ley del paralelogramo es simple: la suma de los cuadrados formados en las diagonales de un paralelogramo es igual a la suma de los cuadrados formados en sus cuatro lados. En geometría plana (1) es una consecuencia fácil de la Ley de los Cosenos. Cuando el paralelogramo resulta ser un rectángulo, sus diagonales coinciden, por lo que (1) se reduce al teorema de Pitágoras.

Vídeos de Ley del paralelogramo