Continuidad de una función

Una función continua, como su nombre indica, es una función cuya gráfica es continua sin interrupciones ni saltos. Es decir, si somos capaces de dibujar la curva (gráfica) de una función sin ni siquiera levantar el lápiz, entonces decimos que la función es continua. El estudio de la continuidad de una función es muy importante en el cálculo, ya que una función no puede ser diferenciable si no es continua.

Continuidad de una función

Se dice que una función f(x) es una función continua en cálculo en un punto x = a si la curva de la función NO se rompe en el punto x = a. La definición matemática de la continuidad de una función es la siguiente. Una función f(x) es continua en un punto x = a si

f(a) existe
limₓ → ₐ f(x) existe
[es decir, limₓ → ₐ₋ f(x) = limₓ → ₐ₊ f(x)] y
limₓ → ₐ f(x) = f(a)

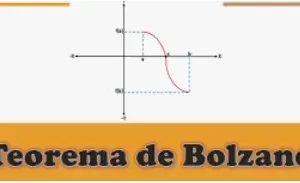
Realmente esta definición da el sentido de que la función no debe tener una ruptura en x = a? Veamos. "limₓ → ₐ f(x) existe" significa, que la función debe acercarse al mismo valor tanto por el lado izquierdo como por el derecho del valor x = a y "limₓ → ₐ f(x) = f(a)" significa que el límite de la función en x = a es igual a f(a). Estas dos condiciones juntas harán que la función sea continua (sin ruptura) en ese punto. Puedes entenderlo en la siguiente figura.

Una función continua es una función en x = a si sus límites del lado izquierdo y del lado derecho son iguales y además estos límites son iguales a f(a).

Leer Función lineal

Se dice que una función es continua a lo largo de un intervalo si es continua en todos y cada uno de los puntos del intervalo. es decir, a lo largo de ese intervalo, la gráfica de la función no debería romperse o saltar.

Propiedades de una función continua

A continuación se presentan algunas propiedades de la continuidad de una función. Si dos funciones f(x) y g(x) son continuas en x = a entonces

f + g, f - g, y fg son continuas en x = a.
f/g también es continua en x = a siempre que g(a) ≠ 0.
Si f es continua en g(a), entonces la función de composición (f o g) también es continua en x = a.
Todas las funciones polinómicas son continuas sobre el conjunto de todos los números reales.
La función de valor absoluto |x| es continua sobre el conjunto de todos los números reales.
Las funciones exponenciales son continuas en todos los números reales.
Las funciones sen x y cos x son continuas en todos los números reales.
Las funciones tan x, cosec x, sec x y cot x son continuas en sus respectivos dominios.
Las funciones como log x, ln x, √x, etc son continuas en sus respectivos dominios.

Teoremas sobre la función continua

Hay varios teoremas sobre una función continua. Aquí están los teoremas más importantes.

Teorema 1: Todas las funciones polinómicas son continuas en (-∞, ∞).
Teorema 2: Las funciones ex, sen x, cos x y arctan x son continuas en (-∞, ∞).
Teorema 3: Si dos funciones f y g son continuas en un intervalo [a, b], entonces f+g, f-g, y fg son continuas en [a, b]. Pero f/g es continua en [a, b] dado que f/g NO es cero en ningún lugar del intervalo.
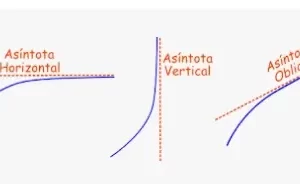
Teorema 4: Una función racional es continua excepto en las asíntotas verticales.

Leer Área semicircunferencia