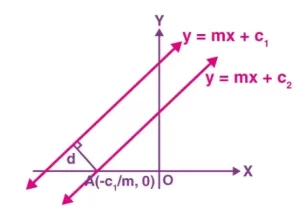
Distancia entre dos rectas paralelas
La longitud de la perpendicular del punto A a la recta (i) es de la misma longitud que la distancia entre dos rectas.
Por tanto, la distancia entre las rectas (i) y (ii) es
|(-m)(-c1/m) + (-c2)|/√(1 + m2) o d = |c1-c2|/√(1+m2).
La distancia d entre dos rectas paralelas y = mx + c1 e y = mx + c2 viene dada por
d = |C1-C2|/√(A2 + B2 )
La distancia entre un punto (x1, y1) y una recta es d= |a1x1+b1y1+c1| / √(a12+b12) ,
donde a1 y b1 son los coeficientes de las variables x e y en la ecuación de la recta.
La ecuación de la recta es
a1x+b1y+c1 = 0
Considerando las siguientes ecuaciones de 2 rectas paralelas, podemos calcular la distancia entre dichas rectas mediante la fórmula de la distancia
ax+by+c = 0
ax+by+c1 = 0
Utilizando las 2 ecuaciones anteriores podemos concluir que
Distancia entre 2 rectas paralelas, d = |c-c1| / √(a2+b2)
Ejemplos resueltos
Ejemplo 1: Hallar la distancia del punto (4, -6) a la recta 2x - 7y - 24 = 0.
Solución:
La recta dada es 2x - 7y - 24 = 0. ...... (1)
Comparando (1) con la ecuación general de la recta Ax + By + C = 0, obtenemos
A = 2, B = -7 y C = -24.
El punto dado es (x1, y1) = (4, -6).
La distancia del punto dado a la recta dada es d = |Ax1 + By1 + C|/√A2+B2 = 26/7,2
= 3.6
Ejemplo 2: Estimar la distancia entre las dos rectas paralelas y=2x+7 e y=2x+5.
Solución:
La distancia entre dos rectas paralelas viene dada por |c1-c2|/√(a2+b2).
Aquí, las ecuaciones de las rectas paralelas son y = 2x + 7 e y = 2x + 5.
Las pendientes son iguales m1 = m2 = 2 y c1 = 7 ,c2 = 5.
Aquí a = 2, b = -1
Entonces, la distancia entre dos rectas paralelas viene dada por
=> |c1-c2| = |7-5|/√(22+12) = 2/√5
Ejemplo 3: Calcular la distancia entre las rectas paralelas 3x+4y+7=0 y 3x+4y-5=0 .
Solución:
La distancia entre dos rectas paralelas viene dada por d = |c1-c2|/√(a2+b2).
Aquí c1 = 7, c2 = -5, a = 3, b = 4
por lo que d = |7 - (-5)|/√(32+42)
= 12/5
Ejemplo 4: Hallar la distancia de la recta 6x - 4y + 36 = 0 al punto (0, 0).
Solución:
La distancia entre un punto (x1, y1) y una recta a1x+b1y+c1 = 0 es
d = |a1x1+b1y1+c1| / √(a12+b12)
Aquí a1 = 6, b1 = -4, c1 = 36, x1 = 0, y1 = 0
por lo que d = 36/√(36 + 16)
= 36/√52
Vídeos de Distancia entre dos rectas paralelas
Entradas Relacionadas
Contenido