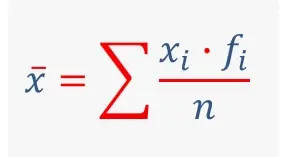Definición de estadística descriptiva

• La estadística descriptiva resume o describe las características de un conjunto de datos.
• La estadística descriptiva consta de dos categorías básicas de medidas: medidas de tendencia central y medidas de variabilidad (o dispersión).
• Las medidas de tendencia central describen el centro de un conjunto de datos.
• Las medidas de variabilidad o dispersión describen la dispersión de los datos dentro del conjunto.

¿Qué es la estadística descriptiva?

Los estadísticos descriptivos, en pocas palabras, ayudan a describir y comprender las características de un conjunto de datos específico ofreciendo breves resúmenes sobre la muestra y las medidas de los datos. Los tipos más reconocidos de estadística descriptiva son las medidas de centro: la media, la mediana y la moda, que se utilizan en casi todos los niveles de matemáticas y estadística. La media, o el promedio, se calcula sumando todas las cifras del conjunto de datos y dividiéndolas por el número de cifras del conjunto.

Por ejemplo, la suma del siguiente conjunto de datos es 20: (2, 3, 4, 5, 6). La media es 4 (20/5). La moda de un conjunto de datos es el valor que aparece con más frecuencia, y la mediana es la cifra situada en el centro del conjunto de datos. Es la cifra que separa las cifras más altas de las más bajas dentro de un conjunto de datos. Sin embargo, hay tipos de estadísticas descriptivas menos comunes que siguen siendo muy importantes.

La gente utiliza las estadísticas descriptivas para reajustar las percepciones cuantitativas difíciles de entender de un gran conjunto de datos en descripciones del tamaño de un bocado. El promedio de notas de un estudiante (GPA), por ejemplo, proporciona una buena comprensión de la estadística descriptiva. La idea de un GPA es que toma puntos de datos de una amplia gama de exámenes, clases y calificaciones, y los promedia juntos para proporcionar una comprensión general del rendimiento académico global de un estudiante. El GPA personal de un estudiante refleja su rendimiento académico medio.

Tipos de estadísticas descriptivas

Todas las estadísticas descriptivas son medidas de tendencia central o medidas de variabilidad, también conocidas como medidas de dispersión.

Tendencia central

Las medidas de tendencia central se centran en los valores medios de los conjuntos de datos, mientras que las medidas de variabilidad se centran en la dispersión de los datos. Estas dos medidas utilizan gráficos, tablas y discusiones generales para ayudar a comprender el significado de los datos analizados.

Las medidas de tendencia central describen la posición central de una distribución para un conjunto de datos. Una persona analiza la frecuencia de cada punto de datos en la distribución y la describe utilizando la media, la mediana o la moda, que mide los patrones más comunes del conjunto de datos analizados.

Medidas de variabilidad

Las medidas de variabilidad (o las medidas de dispersión) ayudan a analizar la dispersión de la distribución de un conjunto de datos. Por ejemplo, aunque las medidas de tendencia central pueden dar a una persona la media de un conjunto de datos, no describen cómo se distribuyen los datos dentro del conjunto.

Así, mientras que la media de los datos puede ser de 65 sobre 100, todavía puede haber puntos de datos tanto en 1 como en 100. Las medidas de variabilidad ayudan a comunicar esto describiendo la forma y la dispersión del conjunto de datos. El rango, los cuartiles, la desviación absoluta y la varianza son ejemplos de medidas de variabilidad.

Considere el siguiente conjunto de datos: 5, 19, 24, 62, 91, 100. El rango de ese conjunto de datos es 95, que se calcula restando el número más bajo (5) del conjunto de datos al más alto (100).

Vídeos de Definición de estadística descriptiva