Ecuación general
La ecuación general de una recta en dos variables de primer grado se representa como
Ax + By +C = 0,
A, B ≠ 0 donde A, B y C son constantes que pertenecen a números reales.
Cuando representamos la ecuación en forma geométrica, siempre obtenemos una recta.
A continuación se representan las fórmulas de la recta en diferentes formas:
Forma de intersección de la pendiente
Sabemos que la ecuación de una recta en forma pendiente-intercepto viene dada como
y = mx + c
Donde m indica la pendiente de la recta y c es la intersección con y
Cuando B ≠ 0 entonces, la ecuación estándar de primer grado Ax + By + C = 0 puede reescribirse en forma pendiente-intercepto como:
y = (- A/B) x - (C/B)
Así, m= -A/B y c = -C/B
Forma de intercepción
El intercepto de una recta es el punto por el que la recta cruza el eje x o el eje y. Supongamos que una recta corta el eje x y el eje y en (a, 0) y (0, b), respectivamente. Entonces, la ecuación de una recta que tiene intersecciones iguales a y b en el eje x y en el eje y, respectivamente, viene dada por
x/a + y/b = 1
Ahora, en el caso de la forma general de la ecuación de la recta, es decir, Ax+By+C = 0, si C ≠ 0, entonces Ax + By + C = 0 puede escribirse como;
x/(-C/A) + y/(-C/B) = 1
donde a = -C/A y b = - C/B
Forma normal
La ecuación de la recta cuya longitud de la perpendicular desde el origen es p y el ángulo que forma la perpendicular con el eje x positivo viene dado por α viene dada por:
x cos α+y sin α = p
Esto se conoce como la forma normal de la recta.
En el caso de la forma general de la recta Ax + By + C = 0 se puede representar en forma normal como:
A cos α = B sin α = - p
De aquí podemos decir que cos α = -p/A y sin α = -p/B.
También se puede deducir que
cos2α + sin2α = (p/A)2 + (p/B)2
1 = p2 (A2 + B2/A2 .B2)
De la ecuación general de una recta Ax + By + C = 0, podemos concluir lo siguiente:
- La pendiente viene dada por -A/B, dado que B ≠ 0.
- La intersección x viene dada por -C/A y la intersección y por -C/B.
- De la discusión anterior se desprende que:
Si se dice que dos puntos (x1, y1) y(x2, y2)se encuentran en el mismo lado de la recta Ax + By + C = 0, entonces las expresiones Ax1+ By1 + C y Ax2 + By2 + C tendrán el mismo signo o de lo contrario estos puntos se encontrarían en los lados opuestos de la recta.
Vídeos de Ecuación general
Entradas Relacionadas
Contenido

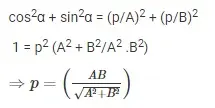 Si se dice que dos puntos (x1, y1) y(x2, y2)se encuentran en el mismo lado de la recta Ax + By + C = 0, entonces las expresiones Ax1+ By1 + C y Ax2 + By2 + C tendrán el mismo signo o de lo contrario estos puntos se encontrarían en los lados opuestos de la recta.
Si se dice que dos puntos (x1, y1) y(x2, y2)se encuentran en el mismo lado de la recta Ax + By + C = 0, entonces las expresiones Ax1+ By1 + C y Ax2 + By2 + C tendrán el mismo signo o de lo contrario estos puntos se encontrarían en los lados opuestos de la recta.