Formulario de centroides

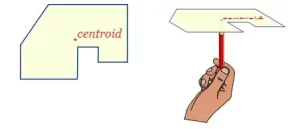
El centroide es la posición media de todos los puntos de un objeto.

Cuando cortamos una forma plana de un trozo de cartulina, ésta se equilibra perfectamente en su centroide.

Centro de gravedad

El centro de gravedad es lo mismo que el centroide cuando la densidad es la misma en todo el conjunto.

El centro de gravedad, el centro de masa y el centroide son los mismos para los sólidos simples.

Suelen estar marcados con una cruz o un punto y a veces con las letras CG o simplemente G.

El centroide de un triángulo es el punto de intersección de las tres medianas del triángulo. Las medianas son los segmentos que unen un vértice con el punto medio del lado opuesto. En esta imagen, el punto G es el centroide del triángulo ABC.

Para localizar el centroide de un triángulo, lo más fácil es dibujar las tres medianas y buscar su punto de intersección. Para dibujar la mediana de un triángulo, primero localiza el punto medio de un lado del triángulo. Dibuja un segmento de línea que conecte este punto con el vértice opuesto. Aquí se muestra un triángulo con una mediana dibujada:

Repite este proceso para los otros dos lados del triángulo. Una vez que hayas dibujado las tres medianas, localiza el punto de intersección de las tres. Este punto es el centroide.

Para un triángulo hecho de un material uniforme, el centroide es el centro de gravedad. Imagina que un artista diseña una escultura en la que varios triángulos de metal se equilibran en los extremos de piezas de alambre.

Propiedades del centroide

El centroide siempre se encuentra dentro del triángulo. Esto es así tanto si el triángulo es agudo, recto u obtuso. En esta imagen, puedes ver que el centroide está dentro de cada uno de los triángulos, aunque todos tengan medidas de ángulo diferentes.

Otra propiedad importante del centroide es que se encuentra a 2/3 de la distancia del vértice al punto medio del lado opuesto. Otra forma de decir esto es que el centroide divide a la mediana en una proporción de 2:1. La distancia del centroide al vértice es el doble de la distancia del centroide al punto medio del lado opuesto al vértice.

Puedes utilizar la distancia del centroide al vértice de un triángulo para encontrar la longitud de todo el segmento de la mediana. También puedes utilizar esta propiedad para localizar el centroide en un triángulo cuando sólo puedes dibujar una mediana.

Vídeos de Formulario de centroides