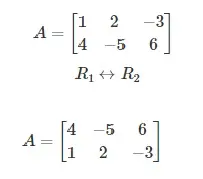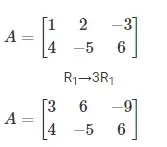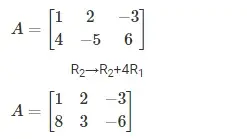Matriz elemental
Una matriz es un conjunto de números dispuestos en forma de filas y columnas. El número de filas y columnas de una matriz se conoce como sus dimensiones, que vienen dadas por mxn, donde m y n representan el número de filas y columnas respectivamente. Aparte de las operaciones matemáticas básicas, hay ciertas operaciones elementales que se pueden realizar sobre una matriz. Las operaciones elementales o de transformación de una matriz son las operaciones que se ejecutan sobre las filas y columnas de una matriz para transformar la matriz dada en una forma diferente con el fin de hacer el cálculo más sencillo.
Sabemos que las operaciones elementales de fila son las operaciones que se realizan sobre las filas de una matriz. Del mismo modo, las operaciones elementales de columna son las operaciones que se realizan sobre las columnas de una matriz.
Las tres operaciones elementales básicas o de transformación de una matriz son:
- Intercambio de dos filas o dos columnas cualesquiera.
- Multiplicación de fila o columna por un número distinto de cero.
- Multiplicación de una fila o columna por un número distinto de cero y sumar el resultado a la otra fila o columna.
Caso 1: Intercambio de dos filas o dos columnas cualesquiera
Se pueden intercambiar 2 columnas (o filas) cualesquiera de una matriz. Si se intercambian las filas ith y jth, se muestra por Ri ↔ Rj y si se intercambian las columnas ith y jth, se muestra por Ci ↔ Cj.
Por ejemplo, dada la matriz A de abajo:
Caso 2: Multiplicación de fila o columna por un número distinto de cero
Los elementos de cualquier fila (o columna) de una matriz pueden multiplicarse por un número distinto de cero. Así, si multiplicamos la fila ith de una matriz por un número no nulo k, simbólicamente se puede denotar por Ri → kRi. Del mismo modo, para la columna viene dada por Ci → kCi.
Por ejemplo, dada la matriz A de abajo:
Caso 3: Multiplicación de una fila o columna por un número no nulo y sumar el resultado a la otra fila o columna
Los elementos de cualquier fila (o columna) pueden sumarse con los elementos correspondientes de otra fila (o columna) que esté multiplicada por un número distinto de cero. Así, si sumamos la fila i de una matriz a la fila j que está multiplicada por un número distinto de cero k, simbólicamente se puede denotar por Ri → Ri + kRj. Del mismo modo, para la columna viene dada por Ci → Ci + kCj.
Por ejemplo, dada la matriz A siguiente: