Derivada de la función inversa
Es tedioso calcular un límite cada vez que necesitamos conocer la derivada de una función. Afortunadamente, podemos desarrollar una pequeña colección de ejemplos y reglas que nos permiten calcular rápidamente la derivada de casi cualquier función que podamos encontrar.
En primer lugar, introducimos una notación diferente para la derivada que puede ser más conveniente en ocasiones.
Hay varias notaciones diferentes para la derivada. Las dos que utilizaremos principalmente son El valor de la derivada en también se puede escribir utilizando dos notaciones diferentes:
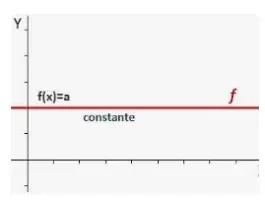
1 - Derivada de una función constante.
La derivada de f(x) = c donde c es una constante viene dada por
f '(x) = 0
Ejemplo
f(x) = - 10 , entonces f '(x) = 0
2 - Derivada de una función potencia (regla de la potencia).
La derivada de f(x) = x r donde r es un número real constante viene dada por
f '(x) = r x r - 1
Ejemplo
f(x) = x -2 , entonces f '(x) = -2 x -3 = -2 / x 3
3 - Derivada de una función multiplicada por una constante.
La derivada de f(x) = c g(x) viene dada por
f '(x) = c g '(x)
Ejemplo
f(x) = 3x 3 ,
sea c = 3 y g(x) = x 3, entonces f '(x) = c g '(x)
= 3 (3x 2) = 9 x 2
4 - Derivada de la suma de funciones (regla de la suma).
La derivada de f(x) = g(x) + h(x) viene dada por
f '(x) = g '(x) + h '(x)
Ejemplo
f(x) = x 2 + 4
si g(x) = x 2 y h(x) = 4, entonces f '(x) = g '(x) + h '(x) = 2x + 0 = 2x
5 - Derivada de la diferencia de funciones.
La derivada de f(x) = g(x) - h(x) viene dada por
f '(x) = g '(x) - h '(x)
Ejemplo
f(x) = x 3 - x -2
si g(x) = x 3 y h(x) = x -2, entonces
f '(x) = g '(x) - h '(x) = 3 x 2 - (-2 x -3) = 3 x 2 + 2x -3
6 - Derivada del producto de dos funciones (regla del producto).
La derivada de f(x) = g(x) h(x) viene dada por
f '(x) = g(x) h '(x) + h(x) g '(x)
Ejemplo
f(x) = (x 2 - 2x) (x - 2)
dejemos que g(x) = (x 2 - 2x) y h(x) = (x - 2), entonces
f '(x) = g(x) h '(x) + h(x) g '(x) = (x 2 - 2x) (1) + (x - 2) (2x - 2)
= x 2 - 2x + 2 x 2 - 6x + 4 = 3 x 2 - 8x + 4
Vídeos de Derivada de la función inversa
Entradas Relacionadas
Contenido