Convexo y cóncavo

Las nociones de concavidad y convexidad se utilizan ampliamente en la teoría económica y también son fundamentales en la teoría de la optimización. Una función de una sola variable es cóncava si cada segmento de línea que une dos puntos de su gráfico no se encuentra por encima del gráfico en ningún punto. Simétricamente, una función de una sola variable es convexa si cada segmento de línea que une dos puntos de su gráfico no se encuentra por debajo del gráfico en ningún punto. Estos conceptos se ilustran en las siguientes figuras.

Una función cóncava

ningún segmento de línea que une
dos puntos de la gráfica
está por encima de la gráfica
en ningún punto

Una función convexa

ningún segmento de línea que una
dos puntos de la gráfica
está por debajo de la gráfica
en cualquier punto

Una función que no es ni
cóncava ni convexa

el segmento de recta mostrado está
por encima de la gráfica en algunos
puntos y por debajo en otros

Sea f una función de una sola variable definida en un intervalo. Entonces f es cóncava si cada segmento de línea que une dos puntos de su gráfica nunca está por encima de la gráfica es convexa si cada segmento de línea que une dos puntos de su gráfica nunca está por debajo de la misma.

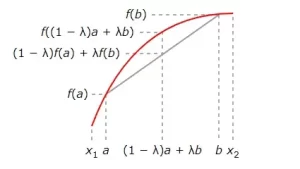
Para que esta definición sea más útil, podemos traducirla en una condición algebraica. Sea f una función definida en el intervalo [x1, x2]. Esta función es cóncava según la definición si, para cada par de números a y b con x1 ≤ a ≤ x2 y x1 ≤ b ≤ x2, el segmento de recta que va de (a, f(a)) a (b, f(b)) se encuentra sobre o debajo de la gráfica de la función, como se ilustra en la siguiente figura.

Denotemos la altura del segmento de recta que va de (a, f(a)) a (b, f(b)) en el punto x por ha,b(x). Entonces, según la definición, la función f es cóncava si y sólo si para cada par de números a y b con x1 ≤ a ≤ x2 y x1 ≤ b ≤ x2 tenemos

f(x) ≥ ha,b(x) para todo x con a ≤ x ≤ b. (*)

Ahora, todo punto x con a ≤ x ≤ b puede escribirse como x = (1 - λ)a + λb, donde λ es un número real de 0 a 1. (Cuando λ = 0, tenemos x = a; cuando λ = 1 tenemos x = b.) El hecho de que ha,b sea lineal significa que
ha,b((1 - λ)a + λb) = (1 - λ)ha,b(a) + λha,b(b)

para cualquier valor de λ con 0 ≤ λ ≤ 1. Además, tenemos que ha,b(a) = f(a) y ha,b(b) = f(b) (el segmento de recta coincide con la función en sus puntos extremos), por lo que
ha,b((1 - λ)a + λb) = (1 - λ)f(a) + λf(b).

Por tanto, la condición (*) es equivalente a
f((1-λ)a + λb) ≥ (1 - λ)f(a) + λf(b) para todo λ con 0 ≤ λ ≤ 1.
Podemos hacer un argumento simétrico para una función convexa. Así, la definición de funciones cóncavas y convexas puede reescribirse como sigue.

Sea f una función de una sola variable definida en el intervalo I. Entonces f es

• cóncava si para todo a ∈ I, todo b ∈ I, y todo λ ∈ (0, 1) tenemos
  f((1-λ)a + λb) ≥ (1 - λ)f(a) + λf(b)
• convexo si para todo a ∈ I, todo b ∈ I, y todo λ ∈ (0, 1) tenemos
  f((1-λ)a + λb) ≤ (1 - λ)f(a) + λf(b).

Vídeos de Convexo y cóncavo