Ecuación general de la elipse

Una elipse en matemáticas es el lugar de los puntos en un plano de tal manera que su distancia a un punto fijo tiene una relación constante de "e" con su distancia a una línea fija (menor que 1). La elipse es una parte del segmento cónico, que es la intersección de un cono con un plano que no interseca la base del cono. El punto fijo se llama foco y se denota por S, la relación constante 'e' como la excentricidad, y la línea fija se llama como directriz (d) de la elipse.

Definición de elipse

Una elipse es el lugar de los puntos de un plano cuya suma de las distancias a dos puntos fijos es un valor constante. Los dos puntos fijos se llaman focos de la elipse.

Ecuación de la elipse

La ecuación general de una elipse se utiliza para representar algebraicamente una elipse en el plano de coordenadas. La ecuación de una elipse puede darse como

Partes de una elipse

Repasemos algunos términos importantes relacionados con las diferentes partes de una elipse.

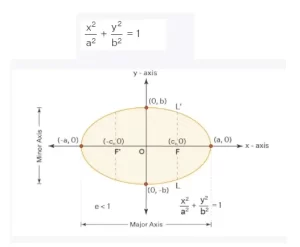
• Foco: La elipse tiene dos focos y sus coordenadas son F(c, o), y F'(-c, 0). La distancia entre los focos es, por tanto, igual a 2c.
• Centro: El punto medio de la línea que une los dos focos se llama centro de la elipse.
• Eje Mayor: La longitud del eje mayor de la elipse es de 2a unidades, y los vértices extremos de este eje mayor son (a, 0), (-a, 0) respectivamente.
• Eje menor: La longitud del eje menor de la elipse es de 2b unidades y los vértices extremos del eje menor son (0, b), y (0, -b) respectivamente.
• Recto mayor: El recto mayor es una línea trazada perpendicularmente al eje transversal de la elipse y que pasa por los focos de la elipse. La longitud del latus rectum de la elipse es 2b2/a.
• Eje transversal: La línea que pasa por los dos focos y el centro de la elipse se llama eje transversal.
• Eje conjugado: La recta que pasa por el centro de la elipse y es perpendicular al eje transversal se llama eje conjugado
• Excentricidad: (e < 1). Es la relación entre la distancia del foco al centro de la elipse y la distancia de un extremo de la elipse al centro de la misma. Si la distancia del foco al centro de la elipse es 'c' y la distancia del extremo de la elipse al centro es 'a', entonces la excentricidad e = c/a.

Vídeos de Ecuación general de la elipse