Ortocentro de un triángulo

El ortocentro variará para los distintos tipos de triángulos, como los isósceles, los equiláteros, los escalenos, los rectángulos, etc. En el caso de un triángulo equilátero, el centroide será el ortocentro. Pero en el caso de otros triángulos, la posición será diferente. El ortocentro no tiene por qué estar sólo dentro del triángulo, en el caso de un triángulo obtuso, está fuera del triángulo.

El ortocentro de un triángulo es el punto en el que se cruzan las perpendiculares trazadas desde los vértices a los lados opuestos del triángulo.

• Para un triángulo de ángulo agudo, el ortocentro se encuentra dentro del triángulo.
• Para el triángulo de ángulo obtuso, el ortocentro se encuentra fuera del triángulo.
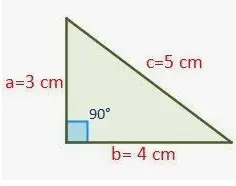
• Para un triángulo rectángulo, el ortocentro se encuentra en el vértice del ángulo recto.

Fórmula del ortocentro

La fórmula del ortocentro se utiliza para encontrar sus coordenadas. Consideremos un triángulo ABC, como se muestra en el diagrama anterior, donde AD, BE y CF son las perpendiculares trazadas desde los vértices A(x1,y1), B(x2,y2) y C(x3,y3), respectivamente. O es el punto de intersección de las tres alturas.

En primer lugar, tenemos que calcular la pendiente de los lados del triángulo, mediante la fórmula

m = y2-y1/x2-x1

Ahora, la pendiente de las altitudes del triángulo ABC será la pendiente perpendicular de la recta.

Pendiente perpendicular de la recta = -1/pendiente de la recta = -1/m

Sea la pendiente de AC dada por mAC. Por lo tanto

mAC = y3-y1/x3-x1

Análogamente, mBC = (y3-y2)/(x3-x2)

Ahora, las pendientes de las respectivas altitudes son

Pendiente de BE, mBE = -1/mAC

Pendiente de AD, mAD = -1/mBC

Ahora vamos a utilizar la ecuación en forma de punto de pendiente de una recta para encontrar las ecuaciones de las rectas que coinciden con BE y AD.

Por lo tanto

mBE = (y-y2)/(x-x2)

mAD = (y-y1)/(x-x1)

Por lo tanto, obtendremos aquí dos ecuaciones que se pueden resolver fácilmente. Así, el valor de x e y dará las coordenadas del ortocentro.

Propiedades del ortocentro

El ortocentro es el punto de intersección de las altitudes trazadas desde los vértices del triángulo a los lados opuestos.

• Para un triángulo agudo, se encuentra dentro del triángulo.
• Para un triángulo obtuso, se encuentra fuera del triángulo.
• Para un triángulo rectángulo, se encuentra en el vértice del ángulo recto.
• El producto de las partes en que el ortocentro divide una altura es el equivalente para las 3 perpendiculares.

Construcción del ortocentro

Para construir el ortocentro de un triángulo, no hay ninguna fórmula particular, sino que tenemos que obtener las coordenadas de los vértices del triángulo. Supongamos que tenemos un triángulo ABC y necesitamos encontrar el ortocentro del mismo.

Entonces, sigue los siguientes pasos;

• Lo primero que tenemos que hacer es encontrar la pendiente del lado BC, utilizando la fórmula de la pendiente, que es, m = y2-y1/x2-x1
• La pendiente de la recta AD es la pendiente perpendicular de BC.
• Ahora, a partir del punto A y de la pendiente de la recta AD, escribe la ecuación de la recta utilizando la fórmula punto-pendiente que es; y2-y1 = m (x2-x1)
• De nuevo encuentra la pendiente del lado AC utilizando la fórmula de la pendiente.
• La pendiente perpendicular de AC es la pendiente de la recta BE.
• Ahora, a partir del punto B y de la pendiente de la recta BE, escribe la ecuación de la recta utilizando la fórmula punto-pendiente que es; y-y1 = m (x-x1)
• Ahora tenemos dos ecuaciones de rectas que son AD y BE.
• Extiende ambas rectas para encontrar el punto de intersección.
• El punto donde se encuentran AD y BE es el ortocentro.

Vídeos de Ortocentro de un triángulo