Teorema del incentro
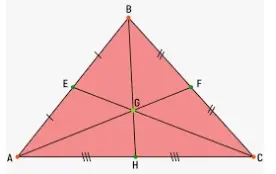
El incentro de un triángulo es el punto de intersección de las tres bisectrices de los ángulos interiores del triángulo. Este punto es equidistante de los lados de un triángulo, ya que el punto de unión del eje central es el punto central del círculo inscrito del triángulo. El incentro de un triángulo también se conoce como el centro del círculo de un triángulo, ya que el círculo más grande podría caber dentro de un triángulo. El círculo inscrito en un triángulo se denomina incentro de un triángulo. El incentro se suele representar con la letra I. El triángulo ABC que se ve en la imagen de abajo muestra el incentro de un triángulo.
Fórmula del incentro de un ángulo de un triángulo
Para calcular el incentro de un ángulo de un triángulo podemos utilizar la fórmula que se menciona a continuación:
Sean E, F y G los puntos donde las bisectrices de los ángulos C, A y B cruzan los lados AB, AC y BC, respectivamente.
Utilizando la propiedad de la suma de ángulos de un triángulo, podemos calcular el incentro de un ángulo del triángulo.
En la figura anterior
∠AIB = 180° - (∠A + ∠B)/2
Donde I es el incentro del triángulo dado.
¿Cómo construir el incentro de un triángulo?
La construcción del incentro de un triángulo es posible con la ayuda de un compás. Estos son los pasos para construir el incentro de un triángulo:
- Paso 1: Coloca uno de los extremos del compás en uno de los vértices del triángulo. El otro extremo del compás está en uno de los lados del triángulo.
- Paso 2: Dibuja dos arcos en dos lados del triángulo utilizando el compás.
- Paso 3: Utilizando la misma anchura que antes, dibuja dos arcos en el interior del triángulo de forma que se crucen desde el punto en que cada arco cruza el lado.
- Paso 4: Dibuja una línea desde el vértice del triángulo hasta donde se cruzan los dos arcos del interior del triángulo.
- Paso 5: Repite el mismo proceso desde el otro vértice del triángulo.
- Paso 6: El punto en el que las dos líneas se encuentran o se cruzan es el incentro del triángulo.
Vídeos de Teorema del incentro
Contenido