Superficies de revolución

Una superficie de revolución es una superficie en el espacio euclidiano creada al girar una curva (la generatriz) alrededor de un eje de rotación. Ejemplos de superficies de revolución generadas por una recta son las superficies cilíndricas y cónicas, dependiendo de si la recta es o no paralela al eje.

¿Qué es una superficie en química?

La superficie de un objeto sólido es una medida del área total que ocupa la superficie del objeto.

¿Es un cilindro una superficie de revolución?

El cilindro de revolución es la superficie generada por la revolución de una línea paralela a un eje, alrededor de este eje. El cilindro se puede desarrollar mediante la asignación de un punto M al punto del plano con coordenadas cartesianas .

¿Para qué sirve la superficie?

El área de la superficie de un objeto tridimensional es el área total de todas sus superficies. El área de la superficie es importante para conocer situaciones en las que queremos envolver algo, pintar algo y, eventualmente, mientras construimos cosas para obtener el mejor diseño posible.

¿Cuál es un ejemplo de superficie de revolución?

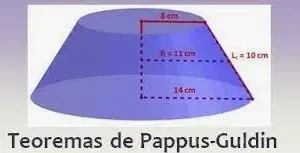
Superficie de revolución. Una superficie de revolución es una superficie generada por la rotación de una curva bidimensional alrededor de un eje. Por tanto, la superficie resultante siempre tiene simetría acimutal. Ejemplos de superficies de revolución son la superficie de la manzana, el cono (excluyendo la base), el tronco de cono (excluyendo los extremos), el cilindro (excluyendo los extremos).

¿La superficie de revolución es siempre de simetría acimutal?

Una superficie de revolución es una superficie generada al girar una curva bidimensional alrededor de un eje. Por lo tanto, la superficie resultante siempre tiene simetría azimutal.

¿Cómo se crea una superficie de revolución en el espacio euclidiano?

Una superficie de revolución es una superficie en el espacio euclidiano creada mediante la rotación de una curva (la generatriz) alrededor de un eje de rotación.

¿Cómo se genera una superficie de revolución en el escalar?

Para generar una superficie de revolución a partir de cualquier función escalar bidimensional y = f(x), basta con hacer de u el parámetro de la función, establecer la función del eje de rotación simplemente como u, y luego utilizar v para girar la función alrededor del eje estableciendo las otras dos funciones iguales a f(u) sen v y f(u) cos v.

Vídeos de Superficies de revolución