Propiedades de la elipse 

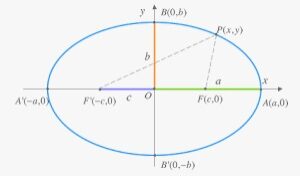
La elipse es un miembro de la sección cónica y tiene características similares a las del círculo. La elipse, a diferencia del círculo, tiene forma ovalada. El lugar de los puntos está representado por una elipse con una excentricidad menor que uno, y la suma de sus distancias a los dos focos de la elipse es un valor constante.

La elipse es una porción del segmento cónico, que es el punto donde un cono se encuentra con un plano que no cruza la base del cono. El foco se designa con S, la relación constante "e" se conoce como excentricidad, y la línea fija se conoce como la directriz (d) de la elipse.La longitud del límite de una elipse es su perímetro. También se conoce como la circunferencia de la elipse. La longitud de la línea continua que forma el límite de la elipse es su perímetro. Desgraciadamente, a diferencia de otras formas, no existe un método para calcular el perímetro exacto (o preciso) de una elipse. Sin embargo, existen numerosas fórmulas de aproximación para calcular el valor aproximado del perímetro, como por ejemplo

• Fórmulas de aproximación
• Fórmulas de Ramanujan
• Fórmulas que hacen uso de series infinitas
• Fórmulas que incorporan la integración

Propiedades de la elipse 

Hay una serie de características que distinguen a la elipse de otras formas comparables. Éstas son las propiedades de una elipse:

• Una elipse se forma cuando un plano interseca a un cono en su ángulo base.
• En toda elipse hay dos focos o puntos focales.
• Las distancias entre cualquier punto de la elipse y los dos focos suman un valor constante.
• Todas las elipses tienen un centro y un eje mayor y menor.

Área de la elipse

El área del círculo se calcula en función de su radio, pero el área de la elipse depende de la longitud del eje menor y del eje mayor.

Área del círculo = πr2

Y

Área de la elipse = Pie(π) x Semieje mayor x Semieje menorÁrea de la elipse = π.a.bDonde el valor de pie (π) = 22/7 ó 3,14

Perímetro de la elipse

El perímetro de una elipse puede definirse como la distancia total que recorre su límite exterior. En el caso de una circunferencia, es muy fácil encontrar su perímetro, ya que la distancia del centro a cualquier punto del lugar de una circunferencia es la misma. Pero en el caso de una elipse, tenemos dos ejes, el mayor y el menor, que pasan por el centro y se cruzan.

Vídeos de Volumen de un octaedro