Volumen de un tronco de pirámide

Llegados a este punto, deberías saber qué es una pirámide, si no es así, tenemos un recurso aparte para la pirámide y deberías consultarlo primero. Imagina una pirámide, el punto que hace que tenga una forma perfecta es el vértice. Sabemos que parece satisfactorio, pero queremos que cortes el vértice y entonces, la pirámide tendrá un aspecto como el de abajo:

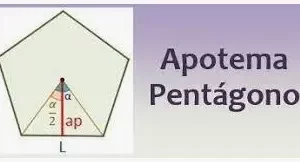
Sí, se llamará pirámide, pero ésta no es una pirámide normal que hayas visto. Esta es especial y los matemáticos le dieron un hermoso nombre que es "pirámide truncada". Una pirámide truncada es el resultado de cortar una pirámide por un plano paralelo a la base y separar la parte que contiene el vértice. Las caras laterales de una pirámide truncada son trapecios. La altura de una pirámide truncada es la distancia perpendicular entre las bases y la apotema es la altura de cualquiera de sus lados.

El volumen de la pirámide es el espacio que ocupa (o) se define como el número de cubos unitarios que pueden caber en ella. Una pirámide es un poliedro, ya que sus caras están formadas por polígonos. Hay diferentes tipos de pirámides, como la pirámide triangular, la pirámide cuadrada, la pirámide rectangular, la pirámide pentagonal, etc., que reciben el nombre de su base, es decir, si la base de una pirámide es un cuadrado, se llama pirámide cuadrada. Todas las caras laterales de una pirámide son triángulos en los que un lado de cada triángulo se funde con un lado de la base.

¿Qué es el volumen de una pirámide?

El volumen de una pirámide se refiere al espacio encerrado entre sus caras. El volumen de cualquier pirámide es siempre un tercio del volumen de un prisma cuando las bases del prisma y de la pirámide son congruentes y las alturas de la pirámide y del prisma son también iguales, es decir, tres pirámides idénticas de cualquier tipo pueden disponerse para formar un prisma del mismo tipo de manera que las alturas de la pirámide y del prisma sean iguales y sus bases sean congruentes, es decir, tres pirámides rectangulares pueden disponerse para formar un prisma rectangular.

Podemos entenderlo con la siguiente actividad. Toma una pirámide rectangular llena de arena y coge un prisma rectangular vacío cuya base y altura sean iguales a las de la pirámide. Vierte la arena de la pirámide en el prisma, podemos ver que el prisma está exactamente un tercio lleno.

Fórmula del volumen de una pirámide

Consideremos una pirámide y un prisma, cada uno de los cuales tiene un área de base "B" y una altura "h". Sabemos que el volumen de un prisma se obtiene multiplicando su base por su altura, es decir, el volumen del prisma es Bh. En el apartado anterior hemos visto que el volumen de la pirámide es un tercio del volumen del prisma correspondiente (es decir, sus bases y alturas son congruentes). Así pues,

Volumen de la pirámide = (1/3) (Bh), donde

B = Área de la base de la pirámide
h = Altura de la pirámide (que también se llama "altitud")

Vídeos de Volumen de un tronco de pirámide