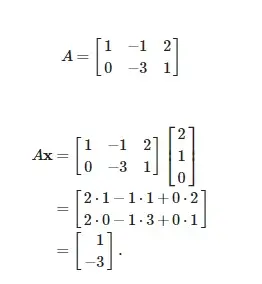Vectores

Cuando multiplicamos dos o más vectores, es importante determinar si queremos un producto que tenga una cantidad escalar o vectorial. La técnica que tendremos que aplicar depende de nuestra respuesta a esa pregunta.

En realidad hay tres productos posibles en la multiplicación de vectores: el vector multiplicado por un factor escalar, el producto punto (o escalar) y el producto cruzado (o vectorial).

• A estas alturas, deberíamos haber aprendido a distribuir factores escalares a un vector, y ése es el primer procedimiento.
• Asegúrate de revisar los enlaces que hemos incluido en la primera sección.
• El producto punto o conocido como producto escalar, como has adivinado, devuelve una cantidad escalar.
• Del mismo modo, el producto cruzado devuelve una cantidad vectorial.

Un vector relaciona dos puntos determinados. Es una cantidad matemática que tiene tanto la magnitud como la dirección.

Multiplicación de vectores

La multiplicación de vectores puede ser de dos tipos:

(i) Multiplicación escalar

(ii) Multiplicación vectorial

Para definir la multiplicación entre una matriz A y un vector x (es decir, el producto matriz-vector), necesitamos ver el vector como una matriz de columnas. Definimos el producto matriz-vector sólo para el caso de que el número de columnas de A sea igual al número de filas de x. Así, si A es una matriz m×n (es decir, con n columnas), el producto Ax se define para vectores de n×1 columnas x. Si dejamos que Ax=b, entonces b es un vector de m×1 columnas. En otras palabras, el número de filas de A (que puede ser cualquiera) determina el número de filas del producto b.

La fórmula general de un producto matriz-vector es:

Vídeos de Multiplicación de vectores