Ángulo suplementario

Por ejemplo, el ángulo 130° y el ángulo 50° son ángulos suplementarios porque la suma de 130° y 50° es igual a 180°. Del mismo modo, los ángulos complementarios suman 90 grados. Los dos ángulos complementarios, si se unen, forman una línea recta y un ángulo recto. Pero hay que tener en cuenta que los dos ángulos complementarios no tienen por qué estar uno al lado del otro. Así, dos ángulos cualesquiera pueden ser suplementarios, si su suma es igual a 180°. La geometría es una de las ramas importantes de las matemáticas que se ocupa del estudio de las diferentes formas. Inicia el estudio de las líneas y los ángulos. Una línea recta es una línea sin curvas y se define como la distancia más corta entre dos puntos. Un ángulo se forma cuando el segmento de la línea se encuentra en un punto.

¿Qué son los ángulos suplementarios?

En matemáticas, el significado de suplementario está relacionado con los ángulos que forman un ángulo recto juntos. Es decir, se dice que dos ángulos son suplementarios cuando suman 180 grados. Dos ángulos son suplementarios si

• Uno de sus ángulos es un ángulo agudo y otro es un ángulo obtuso.
• Ambos ángulos son ángulos rectos.
• Esto significa que ∠A + ∠B = 180°.

Observa la siguiente figura para entender mejor el par de ángulos que son complementarios.

.

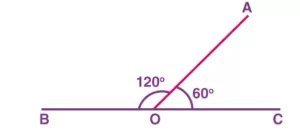
Ejemplos de ángulos suplementarios

Algunos de los ejemplos de ángulos suplementarios son

120° + 60° = 180°
90° + 90° = 180°
140° + 40° = 180°
96° + 84° = 180°

Propiedades de los ángulos suplementarios

Las propiedades importantes de los ángulos suplementarios son:

• Se dice que los dos ángulos son suplementarios cuando suman 180°.
• Los dos ángulos juntos forman una línea recta, pero no es necesario que los ángulos estén juntos.
• La "S" de los ángulos suplementarios significa la línea "Recta". Esto significa que forman 180°.

Ángulos suplementarios adyacentes y no adyacentes

Hay dos tipos de ángulos suplementarios:

• Ángulos suplementarios adyacentes
• Ángulos suplementarios no adyacentes
• Ángulos suplementarios adyacentes

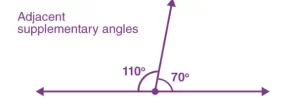
Los ángulos suplementarios que tienen un brazo y un vértice común se llaman ángulos suplementarios adyacentes. Los ángulos suplementarios adyacentes comparten el segmento de línea y el vértice común entre sí.

Por ejemplo, los ángulos suplementarios 110° y 70°, en la figura dada, son adyacentes entre sí.

Ángulos suplementarios no adyacentes

Los ángulos suplementarios que no tienen un brazo y un vértice comunes se denominan ángulos suplementarios no adyacentes. Los ángulos suplementarios no adyacentes no comparten el segmento de línea o el vértice entre sí.

Por ejemplo, los ángulos suplementarios 130° y 50°, en la figura dada, son no adyacentes entre sí.

¿Cómo encontrar los ángulos suplementarios?

Como sabemos, si la suma de dos ángulos es igual a 180°, entonces son ángulos suplementarios. Se dice que cada uno de los ángulos es suplemento de otro ángulo. Por lo tanto, podemos determinar el suplemento de un ángulo, restándolo de 180°.

Por ejemplo, si hubiera dado que dos ángulos que forman ángulos suplementarios. Si un ángulo es ∠A entonces otro ángulo ∠B es su suplemento. Por lo tanto,

∠A = 180° - ∠B (o)

∠B = 180° - ∠A

Vídeos de Ángulo suplementario