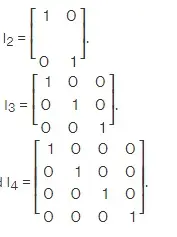Que es una matriz identidad
Una matriz identidad es una matriz cuadrada en la que cada uno de los elementos de su diagonal principal es un 1 y cada uno de los otros elementos es un 0. También se conoce como matriz unidad. Representamos una matriz identidad de orden n × n (o n) como In. A veces la denotamos simplemente como I.
Definición de matriz identidad
La definición matemática de una matriz identidad es
In (o) I = [ai j ] n × n donde a i j = 1 cuando i = j, y a i j = 0 cuando i ≠ j.
Una matriz identidad en general es una identidad con respecto a la multiplicación. Así, para cualquier matriz A
AI = IA = A
es decir, al multiplicar cualquier matriz A por la matriz identidad del mismo orden, obtenemos la misma matriz que el producto y de ahí el nombre de "identidad" para ella.
Definición de matriz identidad y ejemplos. Una matriz identidad es una matriz en la que todos los elementos de la diagonal principal son 1s y el resto de elementos son ceros.
Matriz identidad de diferentes órdenes
A continuación se muestran algunos ejemplos de matrices de identidad de diferentes órdenes. Nótese que una matriz identidad es siempre una matriz cuadrada.
Propiedades de la matriz identidad
Aquí están las propiedades de la matriz identidad basadas en su definición.
- Toda matriz identidad es una matriz cuadrada.
- Toda matriz identidad es una matriz diagonal, ya que sólo los elementos de su diagonal principal son ceros.
- Toda matriz identidad es una matriz escalar ya que todos los elementos de su diagonal principal son iguales y todos los demás elementos son ceros.
- Al multiplicar una matriz identidad con cualquier otra matriz se obtiene la misma matriz.
- El determinante de toda matriz identidad es 1.
- Una matriz identidad es simétrica ya que IT = I.
- La inversa de la matriz identidad es ella misma como I - I-1 = I-1 - I = I.
- Es decir, el cuadrado de la matriz identidad es igual a sí mismo, el cubo de la matriz identidad es igual a sí mismo, y así sucesivamente.
- Al multiplicar una matriz con su inversa, obtenemos una matriz identidad (Veamos esto en la siguiente sección).
Encontrar la matriz inversa usando la matriz identidad
La inversa de una matriz A (que se escribe como A-1) es una matriz B (y viceversa) si y sólo si AB = BA = I, donde A, B e I son las matrices cuadradas del mismo orden. Dadas A y B, es fácil comprobar si son inversas entre sí simplemente verificando si AB = BA = I. Pero si se da una matriz A, ¿cómo podemos encontrar su inversa B? Podemos encontrar la matriz inversa de una matriz siguiendo los siguientes pasos:
- Paso 1: Escribimos una matriz aumentada con la matriz dada uniéndola a la matriz identidad del mismo orden y separamos estas dos matrices por una línea.
- Paso 2: Aplicamos operaciones de fila con el objetivo de convertir la matriz del lado izquierdo (que es A) en una matriz identidad.
- Paso 3: La matriz que queda del lado derecho es nuestra matriz inversa.
Notas importantes sobre la matriz identidad
Aquí hay algunos puntos importantes a tener en cuenta que están relacionados con una matriz identidad.
- Si ves una matriz identidad sin ninguna especificación de la operación, entonces por defecto, se debe entender que es una matriz identidad con respecto a la multiplicación.
- Para escribir una matriz identidad de algún orden, primero se escribe una matriz vacía con el orden dado, se escriben 1s en el lugar de los elementos de la diagonal principal, y finalmente se escriben 0s en el lugar de todos los demás elementos.
- Si AB = BA = I, entonces A y B son inversas entre sí.
- Para encontrar la inversa de una matriz, escríbala adosando la matriz identidad del mismo orden a ella en su lado derecho. Aplicar las operaciones de fila a toda la matriz aumentada con el objetivo de que la matriz del lado izquierdo sea la matriz identidad. Entonces la matriz del lado derecho será la inversa de la matriz dada.
Vídeos de Que es una matriz identidad
Entradas Relacionadas
Contenido