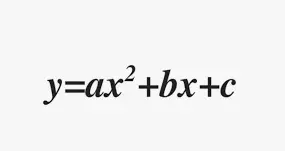Función cuadrática fórmula

Una función cuadrática es una función polinómica con una o más variables en la que el mayor exponente de la variable es dos. Como el término de mayor grado de una función cuadrática es de segundo grado, también se llama polinomio de grado 2. Una función cuadrática tiene un mínimo de un término que es de segundo grado. Es una función algebraica.

Forma estándar de una función cuadrática

La forma estándar de una función cuadrática es de la forma f(x) = ax2 + bx + c, donde a, b y c son números reales con a ≠ 0.

La forma estándar de una función cuadrática se muestra como f de x es igual a ax al cuadrado más b x más c.

Ejemplos de funciones cuadráticas

La ecuación de la función cuadrática es f(x) = ax2 + bx + c, donde a ≠ 0. Veamos algunos ejemplos de funciones cuadráticas:

f(x) = 2x2 + 4x - 5; Aquí a = 2, b = 4, c = -5
f(x) = 3x2 - 9; Aquí a = 3, b = 0, c = -9
f(x) = x2 - x; Aquí a = 1, b = -1, c = 0

Ahora, considera f(x) = 4x-11; Aquí a = 0, por lo tanto f(x) no es una función cuadrática.

Vértice de una función cuadrática

El vértice de una función cuadrática (que tiene forma de U) es donde la función tiene un valor máximo o un valor mínimo. El eje de simetría de la función cuadrática interseca la función (parábola) en el vértice.

El vértice de la función cuadrática es el punto donde tiene el valor máximo o mínimo.

Diferentes formas de la función cuadrática

Una función cuadrática puede tener diferentes formas: forma estándar, forma de vértice y forma de intercepción. A continuación se presentan las formas generales de cada una de ellas:

• Forma estándar: f(x) = ax2 + bx + c, donde a ≠ 0.
• Forma de vértice: f(x) = a(x - h)2 + k, donde a ≠ 0 y (h, k) es el vértice de la parábola que representa la función cuadrática.
• Forma de intercepción: f(x) = a(x - p)(x - q), donde a ≠ 0 y (p, 0) y (q, 0) son los vértices x de la parábola que representa la función cuadrática.

La parábola se abre hacia arriba o hacia abajo según varíe el valor de "a":

• Si a>0, la parábola se abre hacia arriba.
• Si a<0, entonces la parábola se abre hacia abajo.

La forma de la parábola de las funciones cuadráticas se muestra dependiendo del signo de a. Si a es mayor que 0, se abre hacia arriba y si a es menor que 0, se abre hacia abajo.

Siempre podemos convertir una forma en la otra. Podemos convertir fácilmente la forma de vértice o la forma de intercepción en la forma estándar simplemente simplificando las expresiones algebraicas. Veamos cómo convertir la forma estándar en cada una de las formas de vértice e intercepción.

Conversión de la forma estándar de una función cuadrática en forma de vértice

Una función cuadrática f(x) = ax2 + bx + c se puede convertir fácilmente en la forma de vértice f(x) = a (x - h)2 + k utilizando los valores h = -b/2a y k = f(-b/2a). Aquí tienes un ejemplo.

Ejemplo: Convertir la función cuadrática f(x) = 2x2 - 8x + 3 en la forma de vértice.

• Paso - 1: Comparando la función dada con f(x) = ax2 + bx + c, obtenemos a = 2, b = -8, y c = 3.
• Paso - 2: Hallar 'h' mediante la fórmula: h = -b/2a = -(-8)/2(2) = 2.
• Paso - 3: Hallar 'k' mediante la fórmula: k = f(-b/2a) = f(2) = 2(2)2 - 8(2) + 3 = 8 - 16 + 3 = -5.
• Paso - 4: Sustituir los valores en la forma de vértice: f(x) = 2 (x - 2)2 - 5.

Conversión de la forma estándar de la función cuadrática en la forma de intersección

Una función cuadrática f(x) = ax2 + bx + c puede convertirse fácilmente en la forma de vértice f(x) = a (x - p)(x - q) utilizando los valores de p y q (interceptos de x) al resolver la ecuación cuadrática ax2 + bx + c = 0.

Ejemplo: Convertir la función cuadrática f(x) = x2 - 5x + 6 en la forma de intercepto.

• Paso - 1: Comparando la función dada con f(x) = ax2 + bx + c, obtenemos a = 1.
• Paso - 2: Resolver la ecuación cuadrática: x2 - 5x + 6 = 0
  Al factorizar la parte del lado izquierdo, obtenemos
  (x - 3) (x - 2) = 0
  x = 3, x = 2
• Paso - 3: Sustituir los valores en la forma de intercepción: f(x) = 1 (x - 3)(x - 2).

Dominio y rango de la función cuadrática

El dominio de la función cuadrática es el conjunto de todos los valores de x que hacen que la función esté definida y el rango de una función cuadrática es el conjunto de todos los valores de y que la función da como resultado al sustituir diferentes valores de x.

Dominio de la función cuadrática

Una función cuadrática es una función polinómica que está definida para todos los valores reales de x. Por tanto, el dominio de una función cuadrática es el conjunto de los números reales, es decir, R. En notación de intervalo, el dominio de cualquier función cuadrática es (-∞, ∞).

Rango de la función cuadrática

El rango de la función cuadrática depende del lado de apertura de la gráfica y del vértice. Por lo tanto, busca los valores más bajos y más altos de f(x) en la gráfica de la función para determinar el rango de la función cuadrática. El rango de cualquier función cuadrática con vértice (h, k) y la ecuación f(x) = a(x - h)2 + k es

• y ≥ k (o) [k, ∞) cuando a > 0 (ya que la parábola se abre cuando a > 0).
• y ≤ k (o) (-∞, k] cuando a < 0 (ya que la parábola se abre hacia abajo cuando a < 0).

Vídeos de Función cuadrática fórmula