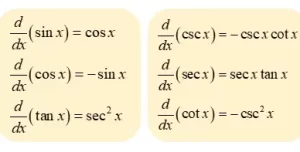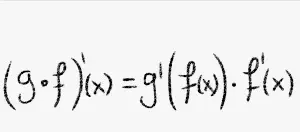Derivadas trigonométricas

Llegando a la pregunta de qué son las derivadas trigonométricas y qué son, las derivadas de las funciones trigonométricas implican seis números. Son la cosecante (cscx), la secante (secx), la cotangente (cotx), la tangente (tanx), el coseno (cosx) y el seno (sinx). Estas funciones se pueden someter al proceso de diferenciación y se pueden encontrar sus correspondientes derivadas. Se conocen como funciones continuas. Es posible encontrar la derivada de una función trigonométrica mediante el proceso de diferenciación. También se denomina proceso de diferenciación a la velocidad a la que puede cambiar una variable.

Es posible demostrar desde los primeros principios que las derivadas de las funciones tangente, coseno y seno están dadas como d(tanx)/dx=sec2x, d(cosx)/dx=sinx, y d(sinx)/dx=cosx. La derivada de una función trigonométrica se puede encontrar utilizando el álgebra. En cualquier valor de x y a partir de la expresión general de la pendiente de una curva, el alumno puede diferenciar una función. Esto permitirá encontrar la derivada de la función concreta en cuestión.

El alumno debe saber que existen derivadas de funciones trigonométricas circulares. Se pueden evaluar mediante el uso de cos(x) y sin(x). Aquí se aplica la regla del cociente para diferenciar la función. La expresión que resulta de este proceso, conduce a las correspondientes derivadas de la trigonometría.

Trigonometría inversa

Las funciones trigonométricas inversas son las funciones inversas de las razones trigonométricas, es decir, sin, cos, tan, cot, sec, cosec. Estas funciones se utilizan ampliamente en campos como la física, las matemáticas, la ingeniería y otros campos de investigación. Al igual que la suma y la resta son las inversas de la otra, lo mismo ocurre con la inversa de las funciones trigonométricas.

sin θ = x

⇒ θ = sin-1x

Representación de las funciones trigonométricas inversas

Se representan sumando arco en prefijo o sumando -1 a la potencia.

El seno inverso se puede escribir de dos maneras:

sin-1 x
arcsin x

Lo mismo ocurre con cos y tan.

Nota: No confundas sin-1 x con (sin x)-1. Son diferentes. Escribir sin-1 x es una forma de escribir el seno inverso mientras que (sin x)-1 significa 1/sin x.

Diferenciación implícita

La diferenciación implícita es un método que hace uso de la regla de la cadena para diferenciar funciones definidas implícitamente. Generalmente no es fácil encontrar la función explícitamente y luego diferenciarla. En cambio, podemos diferenciar totalmente f(x, y) y luego resolver el resto de la ecuación para encontrar el valor de f'(x). Incluso cuando es posible resolver explícitamente la ecuación original, la fórmula resultante de la diferenciación total es, en general, mucho más sencilla y fácil de usar.

Vídeos de Derivadas trigonométricas