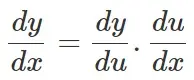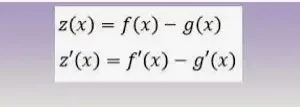Regla de la cadena formula
En el cálculo diferencial, la regla de la cadena es una fórmula utilizada para encontrar la derivada de una función compuesta. Si y = f(g(x)), entonces, según la regla de la cadena, la tasa de cambio instantánea de la función 'f' con respecto a 'g' y 'g' con respecto a x da como resultado una tasa de cambio instantánea de 'f' con respecto a 'x'. Por tanto, la derivada de y vendrá dada como, y' = f'(g(x)).g'(x). La regla de la cadena es una de las reglas importantes en la diferenciación.
La regla aplicada para encontrar la derivada de la función compuesta (por ejemplo, cos 2x, log 2x, etc.) se conoce básicamente como regla de la cadena. También se llama regla de la función compuesta. La regla de la cadena sólo es aplicable a las funciones compuestas. Por lo tanto, antes de comenzar con la fórmula de la regla de la cadena, vamos a entender el significado de la función compuesta y cómo se puede diferenciar.
Fórmula de la regla de la cadena
La fórmula de la regla de la cadena para la función y = f(x), donde f(x) es una función compuesta tal que x = g(t), se da como:
Esta es la forma estándar de la fórmula de la regla de la cadena de la diferenciación.
Otra fórmula de la regla de la cadena está representada por:
y' = d/dx ( f(g(x) ) = f' (g(x)) - g' (x)
Función compuesta para la regla de la cadena
Una función compuesta se denota como:
(niebla)(x) = f(g(x))
Supongamos que f(x) y g(x) son dos funciones diferenciables, de manera que la derivada de una función compuesta f(g(x)) puede expresarse como
(niebla)′ = (f′o g) × g′
Esto se puede entender mejor a partir del ejemplo que se da a continuación:
Consideremos que f(x) = ex2 + 4 y g(x) = x2 + 4
Por tanto, f'(x) = 2x ex2 y g'(x) = 2x
Ahora, la derivada de la función compuesta de f(x) y g(x) se puede escribir como
(niebla)′ = (f′o g) × g′
Sea g(x) = k entonces f(x) = ek {donde k = x2 + 4}
⇒ (f′o g) = ek y g′ = 2x
⇒(niebla)′ = ek × 2x = ex2 + 4 × 2x
Regla de la cadena en la diferenciación
Sea f una función de valor real que es una composición de dos funciones u y v tales que
f = v(u(x))
Supongamos que u(x) = t
Ahora bien, si las funciones u y v son diferenciables y existen dt/dx y dv/dt, entonces la función compuesta f(x) también es diferenciable. Esto puede hacerse como se indica a continuación.
Utilizando la notación de Leibnitz, podemos expresar la diferenciación de la función anterior como
df/dx = (dv/dt) × (dt/dx)
Como su nombre indica, la regla de la cadena significa diferenciar los términos uno a uno en forma de cadena, empezando por la función más externa a la más interna. En términos sencillos, para diferenciar una función compuesta en cualquier punto de su dominio, primero hay que diferenciar la parte exterior (es decir, la función que encierra alguna otra función) y luego multiplicarla por la función derivada de la función interior. Así obtendremos la diferenciación deseada.
Vídeos de Regla de la cadena fórmula
Entradas Relacionadas
Contenido