Diagonales de un polígono

Puede haber numerosos polígonos de lados y pueden ser regulares (de igual longitud y ángulos interiores) o irregulares. Un polígono puede clasificarse además como cóncavo o convexo en función de sus ángulos interiores. Si los ángulos interiores son menores de 180 grados, el polígono es convexo, de lo contrario, es un polígono cóncavo. Hay que tener en cuenta que los lados de un polígono son siempre una línea recta.

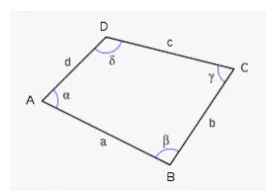
En un polígono, la diagonal es el segmento de línea que une dos vértices no adyacentes. Un hecho interesante sobre las diagonales de un polígono es que en los polígonos cóncavos, al menos una diagonal está realmente fuera del polígono.

Ahora, para un polígono de "n" lados, el número de diagonales se puede obtener mediante la siguiente fórmula:

Número de diagonales = n(n-3)/2

Esta fórmula se forma simplemente por la combinación de diagonales que cada vértice envía a otro vértice y luego se resta el total de lados. Es decir, un polígono de n lados tiene n vértices que se pueden unir entre sí de nC2 maneras.

Ahora al restar n con nC2 formas, la fórmula que se obtiene es n(n-3)/2.

Por ejemplo, en un hexágono, los lados totales son 6. Por tanto, el total de diagonales será 6(6-3)/2 = 9.

Diagonal- Polígonos Diagonales

Una diagonal es un segmento de un polígono que une dos vértices no consecutivos. En un polígono, el número de diagonales que se pueden trazar desde cualquier vértice es tres menos que el número de lados. Multiplica el número en total de diagonales por vértice (n - 3) por el número de vértices, n, y luego divide por 2 para obtener el número total de diagonales en un polígono (si no, cada diagonal se cuenta dos veces).

Diagonal de un cuadrado

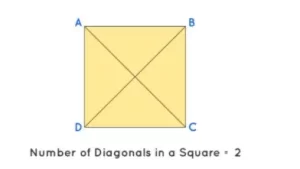
Un cuadrado se define como una figura bidimensional cerrada que tiene cuatro lados y cuatro ángulos. Los lados opuestos son paralelos entre sí y todos los lados tienen la misma longitud. La diagonal de un cuadrado es un segmento de línea que une dos de sus vértices opuestos. Observa el siguiente cuadrado y sus diagonales para relacionar los datos que se dan a continuación:

El número de diagonales de un cuadrado = 2

Al unir los vértices opuestos, obtenemos dos diagonales, AC y BD.
La longitud de las diagonales AC y BD en el cuadrado dado es la misma.
Una diagonal de un cuadrado lo divide en dos triángulos rectángulos iguales, de manera que la diagonal se convierte en la hipotenusa de los triángulos rectángulos así formados.

Diagonal de un rectángulo

La diagonal de un rectángulo es un segmento de línea que une dos de sus vértices no adyacentes. Observa el siguiente rectángulo, en el que AC y BD son las diagonales. Podemos ver que la longitud de AC y BD es la misma. Una diagonal divide un rectángulo en 2 triángulos rectos, y las diagonales se convierten en la hipotenusa de estos triángulos rectángulos.

Longitud de una diagonal

La longitud de una diagonal para cualquier polígono depende del tipo de polígono. No existe una fórmula general para calcular la longitud de una diagonal. Más bien, basándose en las dimensiones del polígono en particular, se puede derivar la fórmula para calcular la longitud de la diagonal. Esta sección cubrirá la fórmula que se utiliza para calcular la longitud de la diagonal para algunos polígonos y sólidos basados en su estructura y dimensiones.

Vídeos de Diagonales de un polígono