Función lineal

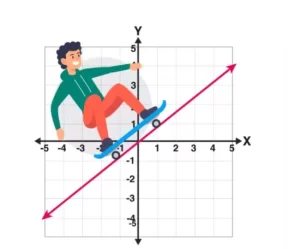
Una función lineal es una función que forma una línea recta en una gráfica. Por lo general, es una función polinómica cuyo grado es como máximo 1 o 0. Aunque las funciones lineales también se representan en términos de cálculo y de álgebra lineal. La única diferencia es la notación de la función. También es necesario conocer un par ordenado escrito en notación de función. Se llama función a f(a), donde a es una variable independiente de la que depende la función. La gráfica de una función lineal tiene una línea recta cuya expresión o fórmula viene dada por

y = f(x) = px + q

Tiene una variable independiente y otra dependiente. La variable independiente es x y la dependiente es y. P es el término constante o la intersección de y y es también el valor de la variable dependiente. Cuando x = 0, q es el coeficiente de la variable independiente conocido como pendiente que da la tasa de cambio de la variable dependiente.

¿Qué es una función no lineal?

Una función que no es lineal se llama función no lineal. Es decir, una función que no forma una línea recta en una gráfica. Los ejemplos de tales funciones son la función exponencial, la función parabólica, las funciones inversas, la función cuadrática, etc. Todas estas funciones no satisfacen la ecuación lineal y = m x + c. La expresión de todas estas funciones es diferente.

Gráfica de una función lineal

Graficar una ecuación lineal implica tres sencillos pasos:

• En primer lugar, hay que encontrar los dos puntos que satisfacen la ecuación y = px+q.
• Ahora trazamos estos puntos en la gráfica o plano X-Y.
• Une los dos puntos en el plano con la ayuda de una recta.

Características de las funciones lineales

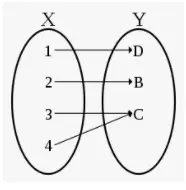
• Relación: Es un conjunto de pares ordenados.
• Variable: Símbolo que muestra una cantidad en una expresión matemática.
• Función lineal: Si cada término es una constante o Es el producto de una constante y también (la primera potencia de) una sola variable, entonces se llama como una ecuación algebraica.
• Función: Una función es una relación entre un conjunto de entradas y un conjunto de salidas admisibles. Tiene la propiedad de que cada entrada está relacionada exactamente con una salida.
• Pendiente: La velocidad a la que una función se desvía de una referencia.
• Dirección: Creciente, decreciente, horizontal o vertical.

Vídeos de Función lineal