Teorema de rolle

El teorema de Rolle debe su nombre a Michel Rolle, un matemático francés. Es un caso especial del teorema del valor medio. El teorema del valor medio de Lagrange también se denomina teorema del valor medio propiamente dicho o primer teorema del valor medio.

Comúnmente, la media se considera como el promedio de los valores dados, pero en el caso de las integrales, el método para encontrar el valor medio de dos funciones diferentes es diferente.

Enunciado del Teorema del Valor Medio de Lagrange:

Si una función f está definida en el intervalo cerrado [a,b] satisfaciendo las siguientes condiciones: i) La función f es continua en el intervalo cerrado [a, b] y ii)La función f es diferenciable en el intervalo abierto (a, b). Entonces existe un valor x = c de forma que f'(c) = [f(b) - f(a)]/(b-a).

El teorema anterior también se conoce como el primer teorema del valor medio. Un caso especial del teorema del valor medio de Lagrange es el teorema de Rolle. Entendamos ahora qué es el Teorema de Rolle.

Enunciado del Teorema de Rolle:

Si una función f está definida en el intervalo cerrado [a, b] de tal manera que satisface las siguientes condiciones: i) La función f es continua en el intervalo cerrado [a, b], ii)La función f es diferenciable en el intervalo abierto (a, b), y iii) Ahora bien, si f (a) = f (b), entonces existe al menos un valor de x, supongamos que este valor es c, que se encuentra entre a y b i. e. (a < c < b ) de tal manera que f'(c) = 0. Precisamente, si una función es continua en el intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b) entonces existe un punto x = c en (a, b) tal que f'(c) = 0.

Matemáticamente, el teorema de Rolle se puede enunciar como Sea f : [a, b] → R continua en [a, b] y diferenciable en (a, b), tal que f(a) = f(b), donde a y b son algunos números reales. Entonces existe algún c en (a, b) tal que f′(c) = 0.

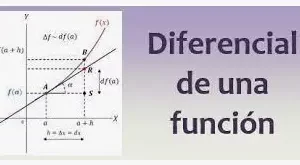
Interpretación geométrica del teorema de Rolle

En la gráfica dada, la curva y = f(x) es continua entre x = a y x = b y en cada punto, dentro del intervalo, es posible trazar una tangente y las ordenadas correspondientes a las abscisas y son iguales entonces existe al menos una tangente a la curva que es paralela al eje x. Algebraicamente, este teorema nos dice que si f (x) representa una función polinómica en x y las dos raíces de la ecuación f(x) = 0 son x = a y x = b, entonces existe al menos una raíz de la ecuación f'(x) = 0 situada entre estos valores. La inversa del teorema de Rolle no es cierta y también es posible que exista más de un valor de x, para el cual el teorema es válido, pero hay una posibilidad cierta de que exista uno de esos valores.

Vídeos de Teorema de rolle

https://www.youtube.com/watch?v=MnlG5oWUEBE