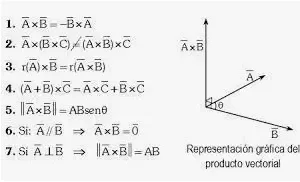
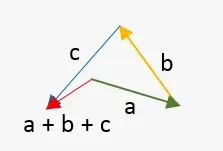
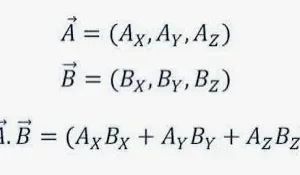Resta de vectores

De la definición anterior se desprende que la sustracción de vectores sólo significa la suma de vectores negativos. Por lo tanto, antes de aprender la sustracción de vectores, es importante repasar los vectores negativos.

Como sabemos, un vector negativo se obtiene multiplicando un vector dado por -1. Esto invierte el sentido del vector.

Digamos que A es un vector que apunta de izquierda a derecha. Multiplicando el vector A por -1 obtenemos -A, que es el negativo del vector A. Aunque la magnitud de los dos vectores A y -A seguirá siendo la misma, el vector negativo -A apuntará de derecha a izquierda.

Cómo restar vectores

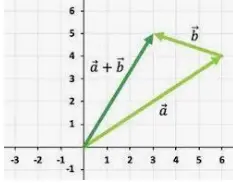
Sabemos que dos vectores, A y B, se pueden sumar usando la adición de vectores, y el vector resultante se puede escribir como R = A + B. De manera similar, si queremos la resta de dos vectores, A y B se expresa matemáticamente como:

R = A - B

Alternativamente como:

R = A +(- B)

Por tanto, restar los dos vectores es lo mismo que sumar el vector A y el negativo del vector B (es decir, B). Los vectores B y -B tendrán la misma magnitud, pero la dirección de -B será opuesta a la del vector B.

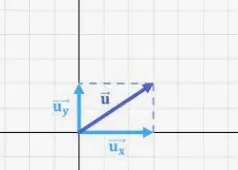
La resta de vectores también funciona cuando los dos vectores se dan en forma de componentes o como vectores columna. Si A = (ax1, ay1) y B = (bx1, by1), entonces la diferencia entre ambos es

R = A - B

Donde las componentes horizontales y verticales del vector resultante R pueden expresarse como:

Rx = ax1 - bx1

y

Ry = ay1 - by1.

Así, el vector resultante puede calcularse simplemente calculando la diferencia de las respectivas componentes horizontal y vertical de los dos vectores originales.

Restar vectores gráficamente

Gráficamente, la regla de cabeza a cola utilizada en la suma de vectores puede adaptarse a la resta de vectores.

Primero, dibuje el vector P, y luego coloque el vector -Q de manera que su cola esté conectada a la cabeza del vector P. Ahora, para encontrar la suma de P y -Q, dibuje el vector resultante R de manera que conecte la cola del vector P con la cabeza del vector -Q.

Matemáticamente, el vector resultante se puede expresar como

R = P - Q

Vídeos de Resta de vectores