Ángulos opuestos

Cuando dos rectas cualquiera se cruzan, se forman diferentes pares de ángulos. Los ángulos que son directamente opuestos entre sí se conocen como ángulos opuestos. También se denominan ángulos verticales o ángulos verticalmente opuestos y son iguales entre sí. Observa la siguiente figura en la que las líneas "a" y "b" se cruzan y forman dos pares de ángulos opuestos. Los ángulos opuestos son ∠1 = ∠3 y ∠2 = ∠4.

Los ángulos verticales se forman cuando dos líneas se encuentran en un punto. Siempre son iguales entre sí. En otras palabras, siempre que dos líneas se cruzan o intersecan, se forman 4 ángulos. Podemos observar que dos ángulos opuestos entre sí son iguales y se llaman ángulos verticales. También se denominan "ángulos verticalmente opuestos", ya que se encuentran uno frente al otro.

Diferencia entre ángulos opuestos y ángulos adyacentes

La intersección de dos rectas cualesquiera da lugar a ángulos adyacentes y opuestos en ellas. Sin embargo, estos dos ángulos son diferentes entre sí y se pueden identificar fácilmente con la ayuda de sus propiedades. Observa la siguiente figura y la tabla que muestra la diferencia entre ángulos opuestos y ángulos adyacentes.

Ángulos opuestos en un paralelogramo

Los ángulos opuestos en un cuadrilátero son aquellos ángulos que se sitúan en diagonal opuestos entre sí. En otras palabras, son los ángulos que están conectados a través de las diagonales. Por ejemplo, en el siguiente paralelogramo ABCD, ∠A y ∠C se llaman ángulos opuestos. Del mismo modo, ∠B y ∠D son ángulos opuestos. Una de las propiedades de un paralelogramo establece que los ángulos opuestos son de igual medida.

Ángulos opuestos en un cuadrilátero cíclico

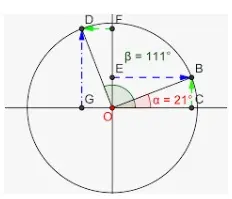
Un cuadrilátero cíclico es un cuadrilátero cuyos vértices se encuentran en una circunferencia y también se conoce como cuadrilátero inscrito en una circunferencia. En otras palabras, es un cuadrilátero que está dentro de una circunferencia y todos sus vértices tocan la circunferencia. Hay muchos teoremas relacionados con un cuadrilátero cíclico y el relacionado con los ángulos opuestos dice que," Los ángulos opuestos en un cuadrilátero cíclico son suplementarios, es decir, la suma de los ángulos opuestos es igual a 180°". Observa la siguiente figura que muestra que los ángulos opuestos en un cuadrilátero cíclico son suplementarios.

Vídeos de Ángulos opuestos