Área polígono irregular
El área de un polígono es el espacio total que encierra la forma. La medición se realiza en unidades cuadradas.
Como sabemos, un polígono puede ser regular o irregular. Los polígonos regulares tienen una dimensión definida en sus lados y, por tanto, sus áreas son fáciles de calcular en comparación con los polígonos irregulares, en los que los lados no tienen una dimensión fija.
El cálculo del área y el perímetro de los polígonos irregulares se puede realizar mediante fórmulas sencillas, al igual que se calculan los polígonos regulares. Veamos las fórmulas:
Área de polígonos irregulares
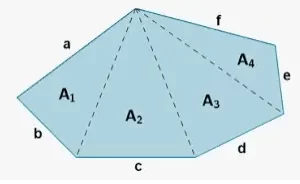
Un polígono irregular es una forma plana cerrada que no tiene lados y ángulos iguales. Por lo tanto, para calcular el área de los polígonos irregulares, dividimos el polígono irregular en un conjunto de polígonos regulares de forma que se conozcan las fórmulas de sus áreas. Consideremos el ejemplo que se presenta a continuación.
Área de polígonos
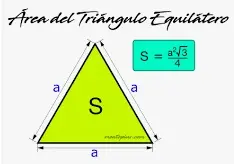
El polígono ABCD es un polígono irregular. Por tanto, podemos dividir el polígono ABCD en dos triángulos ABC y ADC. El área del triángulo se puede obtener mediante:
Área del polígono ABCD = Área del triángulo ABC + Área del triángulo ADC.
Perímetro de los polígonos irregulares
Los polígonos que no tienen lados iguales y ángulos iguales se denominan polígonos irregulares. Así, para calcular el perímetro de los polígonos irregulares, se suman las longitudes de todos los lados del polígono.
- Hallar el perímetro del polígono dado.
Solución: Como podemos ver, el polígono dado es un polígono irregular ya que la longitud de cada lado es diferente (AB = 7 unidades, BC = 8 unidades, CD = 3 unidades y AD = 5 unidades)
Por tanto, el perímetro del polígono irregular vendrá dado por la suma de las longitudes de todos sus lados.
Así, el perímetro de ABCD = AB + BC + CD + AD ⇒ Perímetro de ABCD = (7 + 8 + 3 + 5) unidades = 23 unidades
Por tanto, el perímetro de ABCD es de 23 unidades.
Ejemplo de área de un polígono irregular
Si los tres ángulos interiores de un cuadrilátero son 86°,120° y 40°, ¿cuál es la medida del cuarto ángulo interior?
Solución:
Sabemos que la suma de los ángulos interiores de un polígono irregular = (n - 2) × 180°, donde 'n' es el número de lados
Como es un cuadrilátero, n = 4.
Por tanto, la suma de los ángulos interiores del cuadrilátero = (4 - 2) × 180°= 360°
Sea el cuarto ángulo interior x.
Por tanto, 86° + 120° + 40° + x = 360°
⇒ 246° + x = 360°
⇒ x = 360° - 246°
⇒ x = 114°
El cuarto ángulo interior es 114°.
Vídeos de Área polígono irregular
Entradas Relacionadas
Contenido