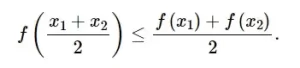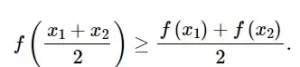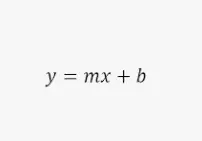Función cóncava

La función y = f (x) se llama convexa hacia abajo (o cóncava hacia arriba) si para dos puntos cualesquiera x1 y x2 en [a, b], se cumple la siguiente desigualdad:

Si esta desigualdad es estricta para cualquier x1, x2 ∈ [a, b], tal que x1 ≠ x2, entonces la función f (x) se llama estrictamente convexa hacia abajo en el intervalo [a, b].

De forma similar, definimos una función cóncava. Una función f (x) se llama convexa hacia arriba (o cóncava hacia abajo) si para dos puntos cualesquiera x1 y x2 en el intervalo [a, b], es válida la siguiente desigualdad:

Si esta desigualdad es estricta para cualquier x1, x2 ∈ [a, b], tal que x1 ≠ x2, entonces la función f (x) se llama estrictamente convexa hacia arriba en el intervalo [a, b].

Interpretación geométrica de la convexidad

El concepto introducido de convexidad tiene una interpretación geométrica sencilla.

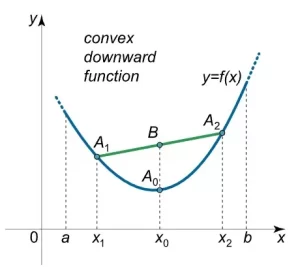
Si una función es convexa hacia abajo (Figura 1 ), el punto medio B de cada cuerda A1A2 se encuentra por encima del correspondiente punto A0 de la gráfica de la función o coincide con este punto.

Del mismo modo, si una función es convexa hacia arriba (Figura 2 ), el punto medio B de cada cuerda A1A2 se encuentra por debajo del correspondiente punto A0 de la gráfica de la función o coincide con este punto.

Las funciones convexas tienen otra propiedad evidente, que está relacionada con la ubicación de la tangente a la gráfica de la función. La función f(x) es convexa hacia abajo en el intervalo [a, b] si y sólo si su gráfica no se encuentra por debajo de la tangente trazada a ella en ningún punto X0 del segmento [a, b] (Figura 3 ).

En matemáticas, el término cóncavo puede aplicarse a formas y funciones. Repasemos qué significa que una forma sea cóncava y qué significa que una función sea cóncava.

Forma cóncava

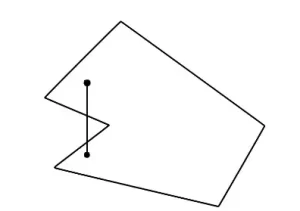
Acabamos de ver que la definición de cóncavo es estar curvado hacia adentro. Así es también como describiríamos una forma cóncava. Una forma que se curva hacia adentro es una forma cóncava. La definición formal de una forma cóncava es una forma en la que es posible dibujar dos puntos dentro de la forma y la línea que conecta los dos puntos va fuera de la forma. Esto se ilustra en la siguiente imagen:

Observa que la forma de la imagen de arriba parece como si estuviera hundida. Como el nombre cóncavo incluye la palabra "cueva", es fácil recordar que una forma cóncava es una forma que parece estar hundida en alguna parte.

Cuando se trata de polígonos (formas creadas con tres o más segmentos de línea), existe otra regla que nos ayuda a reconocer un polígono cóncavo. Es decir, un polígono es cóncavo cuando al menos uno de sus ángulos interiores es mayor de 180 grados.

Consideremos un no ejemplo, como un círculo, que está curvado hacia fuera en todas partes y no parece cóncavo en ninguna parte. Observa la siguiente imagen de un círculo:

Fíjate en que no importa dónde coloques dos puntos dentro de un círculo, la línea que une los dos puntos nunca sale del círculo. Por lo tanto, un círculo no es cóncavo; cuando una forma no es cóncava, la llamamos convexa.

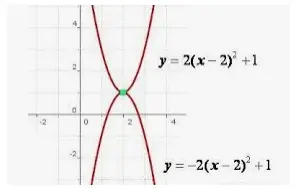
La concavidad de una función tiene que ver con la pendiente de una función. Recordemos que la pendiente de una función es la velocidad a la que la función aumenta o disminuye y se puede encontrar calculando el cambio en y dividido por el cambio en x. Cuando la pendiente de una función es creciente, decimos que la función es cóncava hacia arriba, y cuando la pendiente de una función es decreciente, decimos que la función es cóncava hacia abajo. Esto se ilustra en la siguiente imagen:

Decir que una función es cóncava es sinónimo de decir que una función es cóncava hacia abajo. Por tanto, una función es cóncava cuando la pendiente de la función es decreciente. Por ejemplo, la función y = -x^2 es.

Vídeos de Función cóncava