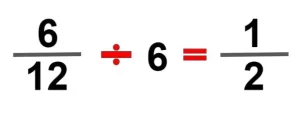Como simplificar fracciones

Cuando se trata de fracciones, lo ideal es tener la forma más simple de esa fracción. Una fracción puede simplificarse si el numerador y el denominador son divisibles por el mismo número. Esto facilita la resolución de cálculos en los que hay que sumar, restar, dividir o multiplicar fracciones.

Veamos el siguiente ejemplo sobre cómo poner las fracciones en su forma más simple:

Simplificar ⁶⁄₁₂

Para que podamos simplificar esta fracción, tenemos que encontrar un número entero que pueda dividirse en 6 y 12. Una buena táctica a tener en cuenta es que el numerador suele ser el número por el que se quiere dividir. En esta situación es cierto, ya que el 6 puede dividirse entre sí mismo y entre el 12.

No siempre podrás simplificar una fracción utilizando el numerador. Para demostrarlo, probemos otro ejemplo:

Simplificar ⁹⁄₁₂

Mientras que 6 se divide en 12, no puede dividirse en 9, lo que significa que no podemos utilizar el mismo proceso que la vez anterior. En este punto, lo mejor es pensar en los horarios. Dividir por 1 sólo nos llevaría a la misma fracción. 2 puede dividirse entre 12 pero no entre 9. Esto nos lleva a 3, que se puede multiplicar por 3 para darnos 9 y por 4 para darnos 12.

⁹⁄₁₂ ÷ 3 = ¾

Cómo simplificar las fracciones algebraicas

Enseñar fracciones simples y cómo simplificarlas puede ser un reto por sí mismo. Cuando se introduce el álgebra en la mezcla, es natural que tu clase se sienta nerviosa. Sin embargo, la simplificación de fracciones algebraicas no es demasiado difícil una vez que se ha desglosado.

Veamos un ejemplo para ver cómo se hace:

²ˣ⁄₄ₓ

Esto puede parecer muy complejo, pero si sabes cómo simplificar fracciones, simplificar fracciones algebraicas es algo natural. Para que podamos simplificar esta fracción, debemos encontrar un número que pueda dividirse tanto en 2 como en 4. Por suerte, el numerador de esta fracción es 2, lo que nos facilita el trabajo. Esto nos lleva a:

²ˣ⁄₄ₓ ÷ 2 = ˣ⁄₂ₓ

Eso ya se ve mucho mejor, pero podemos simplificarlo aún más. Al igual que solemos buscar un número por el que podamos dividir tanto el numerador como el denominador, podemos hacer lo mismo con x. Cuando dividimos nuestro ejemplo por x en ambos lados, obtenemos:

ˣ⁄₂ₓ ÷ x = ½

Puede costar acostumbrarse, pero tiene sentido. Sin embargo, hay fracciones más complicadas que no se pueden resolver en tan pocos pasos. Ésta parece aún más desalentadora, pero te mostraremos cómo se resuelve:

²⁽ˣ⁺¹⁾⁄₄₍ₓ₊₁₎

Puede que te estés rascando la cabeza preguntándote por dónde empezar. Sin embargo, si conoces los fundamentos de la simplificación de fracciones algebraicas, lo conseguirás sin problemas. Lo primero que se te ocurrirá será dividir ambos lados por 2, como hemos hecho antes. Sin embargo, en realidad podemos dividir ambos lados por x+1, lo que nos da

²⁽ˣ⁺¹⁾⁄₄₍ₓ₊₁₎÷ x+1 = ²⁄₄

Ves, ¡sabíamos que lo tenías claro! Ahora sólo queda simplificar aún más esta fracción dividiendo el numerador y el denominador por 2 para obtener:

²⁄₄ ÷ 2 = ½

Es posible que te encuentres simplificando fracciones algebraicas que tienen numerosas expresiones y paréntesis en ellas como:

² ⁽ˣ⁺¹⁾ ⁽ˣ⁺²⁾⁄₄ ₍ₓ₊₁₎ ₍ₓ₊₂₎

Vídeos de Como simplificar fracciones