Fracciones de suma y resta
Todas las fracciones no se pueden sumar o restar fácilmente. Para sumar o restar fracciones existen los siguientes métodos.
- Sumar o restar fracción con el mismo denominador
- Sumar o restar fracción con diferente denominador
- Sumar o restar fracción con número mixto
Suma o resta de fracciones con el mismo denominador
En este método, la suma o la resta de una fracción es muy fácil. Porque los denominadores de las dos fracciones son iguales.
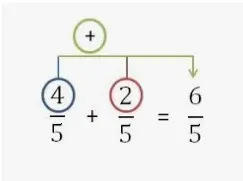
Ejemplo: 2/4 + 3/4 = ?
En las fracciones anteriores, los denominadores son iguales.
2/4 =
1 2
3/4 =
1 2 3
En las fracciones anteriores, la caja está dividida en cuatro partes. Para 2/4 y 3/4, se toman las partes del numerador respectivamente de 4 partes iguales.
A continuación se indican los pasos para sumar fracciones con los mismos denominadores:
Paso 1: Comprueba las fracciones dadas, si los denominadores son iguales o no.
Paso 2: Si los denominadores son iguales, toma los numeradores de las dos fracciones y súmalos o réstalos.
Paso 3: Dar una respuesta final con el denominador.
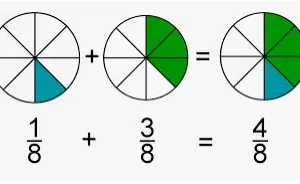
Ejemplo 1: 5/8 + 2/8 = ?
Paso 1: Los denominadores son iguales.
Paso 2: Tomar los numeradores 5 y 2 respectivamente y sumarlos.
= (5+2)/8
Paso 3: Dar la respuesta final.
= 7/8
Ejemplo 2: 5/8 - 2/8 =?
Paso 1: Los denominadores son iguales.
Paso 2: Tomar los numeradores 5 y 2 respectivamente y restar el menor del numerador mayor.
= (5-2)/8
Paso 3: Dar la respuesta final.
= 7/8
Suma o resta de fracciones con distinto denominador
En este método, los denominadores no son iguales en dos fracciones. Por lo tanto, los numeradores y denominadores son diferentes en las dos fracciones. Así que tenemos que hacer que los denominadores sean iguales.
Sumemos dos fracciones, 3/8 y 5/12.
En las fracciones anteriores, los numeradores y los denominadores son diferentes. Veamos la solución paso a paso para la suma de dos fracciones 3/8 y 5/12.
Paso 1: Tomar el mcm de los denominadores de las fracciones anteriores, es decir, 8 y 12 respectivamente.
(LCM es el número más pequeño que se utiliza como múltiplo común de dos números)
24 es un múltiplo común de 8 y 12.
Paso 2: Convertir los denominadores 8 y 12 en 24.
Para 3/8, multiplica el numerador y el denominador por 3 = 3/8 x3/3 = 9/24
Para 5/12, multiplique el numerador y el denominador por 2 = 5/12x 2/2 = 10/24
Paso 3: Ahora, los denominadores de las dos fracciones son iguales.
9/24, 10/24
Paso 4: Toma los numeradores 9 y 10 respectivamente y súmalos.
= (9+10)/24
Paso 5: Da una respuesta final
= 19/24
Se puede seguir un procedimiento similar para restar las fracciones con diferentes denominadores.
Ejemplo: 3/8 - 5/12 =?
Solución:
Paso 1: Los denominadores son diferentes. Entonces, toma el Mínimo Común Múltiplo (LCM).
24 es un múltiplo común de 8 y 12.
Paso 2: Haz que los denominadores sean iguales multiplicando 3/3 por ⅜ y multiplicando 2/2 por 5/12.
3/8 => 3/8 x3/3 = 9/24
5/12 => 5/12x 2/2 = 10/24
Paso 3: Toma los numeradores y resta.
3/8 - 5/12 = 9/24 - 10/24
= (9-10)/24 (resta el numerador menor del mayor)
Paso 4: Respuesta = -1/24
Suma y resta de fracciones mixtas
Una fracción mixta se define como una fracción y un número entero combinados en un número "mixto".
Dependiendo del denominador, existen dos métodos para sumar o restar una fracción mixta.
- Si los mismos denominadores están presentes en la fracción mixta.
- Si hay diferentes denominadores en la fracción mixta.
Suma o resta de fracciones mixtas con el mismo denominador
En este método, la fracción mixta está formada por los mismos denominadores. Para sumar o restar la fracción mixta se siguen los siguientes pasos.
Paso 1: Sumar el número entero de dos fracciones por separado.
Paso 2: Sumar las fracciones por separado.
Paso 3: Combinar el número entero y la fracción ambos.
Paso 3: Convertir la fracción impropia en fracción mixta.
Ejemplo: 3 2/5 + 1 4/5 = ?
Paso 1: Sumar el número entero de dos fracciones por separado
= 3+1 = 4 - (1)
Paso 2: Sumar las fracciones por separado
= 2/5 + 4/5 = 6/5 -- (2)
Paso 3: Combinar las dos ecuaciones (1) y (2)
= 4 6/5 -- (3)
En 4 6/5, 6/5 es una fracción impropia. Por lo tanto, conviértela en una fracción mixta adecuada.
Ecuación (2) --> 6/5 = 1 1/5 -- (3)
Paso 4: Ahora, suma las ecuaciones (1) y (3)
4 + 1 1/5 = 5 1/5
Respuesta = 5 1/5
Suma o resta de fracciones mixtas con distinto denominador
En este método, la fracción mixta consta de diferentes denominadores. Para sumar o restar la fracción mixta se siguen los siguientes pasos.
Ejemplo: 6 3/4 + 3 5/8 = ?
Solución: En las fracciones mixtas anteriores, los denominadores son diferentes. Así que tenemos que hacer que los denominadores sean iguales.
Paso 1: Tomar el MCL de los denominadores de las fracciones anteriores, es decir, 4 y 8 respectivamente.
(LCM es el número más pequeño que se utiliza como múltiplo común de dos números)
8 es un múltiplo común de 4 y 8.
Paso 2: Convertir los denominadores 4 y 8 en 8.
En 3/4, multiplicar el numerador y el denominador por 2 = 3/4 x2/2 = 6/8
En 5/8, multiplicar numerador y denominador por 1 = 5/8x 1/1 = 5/8
(Nota: Debemos hacer con el numerador lo mismo que hacemos con el denominador)
Ahora, los denominadores son iguales en la fracción mixta
6 3/4 + 3 5/8 = 6 6/8 + 3 5/8
Paso 3: Sumar el número entero de dos fracciones por separado
= 6+3 = 9 ---- (1)
Paso 4: Suma las fracciones por separado
= 6/8 + 5/8= 11/8 -- (2)
11/8 es una fracción impropia. Por tanto, conviértelo en una fracción propia.
11/8 = 1 3/8 ----(3)
Paso 5: Combina ambas ecuaciones (1) y (3)
9+ 1 3/8 = 10 3/8
Respuesta: 10 3/8
Vídeos de Fracciones de suma y resta
Entradas Relacionadas
Contenido