Fórmula de vectores

Históricamente, los vectores se utilizaban en geometría, física y mecánica. Sin embargo, con el paso del tiempo, los vectores se han convertido en algo muy utilizado en muchos campos, como el álgebra lineal, la ingeniería, la informática, el análisis estructural y la navegación.

Dado que los vectores expresan dos nociones, la magnitud y la dirección, pueden construir una gran variedad de modelos matemáticos para diversos problemas y escenarios.

Representación geométrica y matemática de los vectores

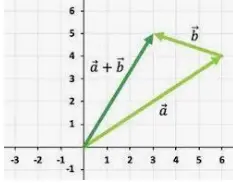
Los vectores pueden ser representados geométricamente por flechas rectas de una longitud específica que apuntan en una dirección específica con puntos específicos de inicio y final. La longitud del vector representa su magnitud, mientras que la dirección indica su sentido respecto a un conjunto de coordenadas. La imagen siguiente es un ejemplo de representación geométrica de un vector.

Considere la siguiente figura en la que A es un vector. |A| representa su longitud (o magnitud), y la punta de flecha que apunta del punto a al punto b representa su dirección. El punto a se llama punto inicial, o de partida, y el punto b se llama punto terminal o final del vector A. Aunque este ejemplo muestra un vector en dos dimensiones, también puede tener tres, cuatro o más dimensiones.

La magnitud del vector es básicamente la misma que la longitud del segmento de línea ab. La dirección del vector es básicamente la misma que la dirección de la flecha.

Algebraicamente, un vector puede expresarse como un par ordenado. Esta representación se llama vector columna. En la imagen siguiente, el vector OA se representa como un vector columna.

OA = (2,3)

Esto significa que el vector está desplazado del origen en dos puntos a lo largo del eje horizontal (eje x) y cuatro puntos a lo largo del eje vertical (eje y).

Los vectores suelen representarse con letras en negrita, como la a o la A. Si no es posible utilizar negrita, como cuando se escriben notas a mano, un vector se representa con una letra con una punta de flecha encima.

Vectores y escalares

Las magnitudes físicas y matemáticas se clasifican como vectores o escalares. Aunque están relacionadas, los vectores y los escalares se utilizan en situaciones diferentes.

Cantidad escalar

Una cantidad escalar tiene magnitud pero no dirección.

Los escalares se representan con letras simples como la a o la A, y suelen estar formados por números reales. Algunos ejemplos comunes de escalares son el tiempo, la velocidad, la energía, la masa, el volumen, el área y la altura.

Cantidades vectoriales

Una cantidad vectorial tiene tanto magnitud como dirección.

A diferencia de las cantidades escalares, que sólo tienen un componente, las cantidades vectoriales constan de dos componentes. Algunos ejemplos comunes de vectores son la velocidad, el desplazamiento y la aceleración.

Para entender mejor la diferencia entre magnitudes escalares y vectoriales, veamos algunos ejemplos:

Identifica si la cantidad dada es un vector o un escalar.

V = 10m, Este

Para clasificar esta cantidad, hay que tener en cuenta las definiciones de vectores y escalares y averiguar cuántos componentes tiene. Primero descomponemos la cantidad dada en sus partes. La cantidad dada tiene una componente de magnitud de |V| = 10m. Además, apunta hacia el Este. Por lo tanto, podemos concluir que la cantidad dada es un vector porque tiene dos componentes.

A = 5 cm

En este ejemplo, sólo está presente la componente de magnitud. Como no se menciona la dirección, esta cantidad es un escalar.

La magnitud del escalar A es 5 cm.

Diferentes tipos de vectores

Los diferentes tipos de vectores utilizados en matemáticas son

• Vector Cero
• Vectores unitarios
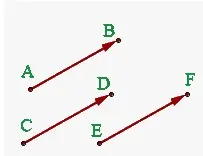
• Vectores iguales
• Vectores de desplazamiento
• Negativo de un Vector
• Vectores de posición
• Vectores co-iniciales
• Vectores colineales
• Vectores coplanares

Vídeos de Fórmula de vectores