Funcion a trozos

Para entender bien qué son las funciones a trozos y cómo podemos construir nuestras propias funciones definidas a trozos, vamos a profundizar primero en su funcionamiento.

Definición de función a trozos

Una función a trozos es una función que está definida por diferentes fórmulas o funciones para cada intervalo dado. También está en el nombre: a trozos. La función está definida por trozos de funciones para cada parte del dominio.

2x, para x > 0
1, para x = 0
-2x, para x < 0

Como se puede ver en el ejemplo anterior, f(x) es una función a trozos porque está definida de forma única para los tres intervalos: x > 0, x = 0 y x < 0.

¿Cómo se leen las funciones a trozos?

Una vez que tenemos una función definida a trozos, podemos interpretarla observando los intervalos dados. Si miramos nuestro ejemplo, podemos leerlo como

Cuando x > 0, f(x) es igual a 2x.
Cuando x = 0, f(x) es igual a 1.
Cuando x < 0, f(x) es igual a -2x.

Cuando te den una gráfica de una función a trozos, asegúrate de observar los intervalos dados en los que f(x) tiene gráficas variadas.

¿Cómo resolver funciones a trozos?

Ahora que hemos aprendido sobre esta función única, ¿cómo nos aseguramos de que devolvemos el valor correcto de la función dada x? Aquí hay consejos para recordar cuando resolvemos y evaluamos funciones a trozos:

• Comprueba dos veces dónde se encuentra x en el intervalo dado.
• Evalúa el valor utilizando la función correspondiente.

Digamos que queremos encontrar f(8) usando la función a trozos que hemos mostrado.

2x, para x > 0

1, para x = 0

-2x, para x < 0

Como 8 es mayor que 0, la función que usaremos para evaluar f(8) es f(x) = 2x. Por lo tanto, tenemos f(8) = 2(8) = 16. Esto también significa que f(-6) = -2(-6) = 12 y f(0) = 1.

¿Cómo se grafican las funciones a trozos?

Como hemos mencionado antes, las funciones a trozos contienen diferentes funciones para cada uno de los intervalos dados. Esto significa que cuando se grafican funciones a trozos, se espera graficar diferentes funciones para cada intervalo también.

Aquí hay algunos recordatorios rápidos cuando se grafican funciones a trozos:

• Ayuda a identificar cómo se vería cada función.
• Para intervalos inclusivos (es decir, x ≥ 0), incluyendo los puntos finales.
• Para intervalos exclusivos (es decir, x < 0), excluye los puntos finales utilizando puntos sin rellenar.

¿Cuáles son las funciones comunes que puedes encontrar al graficar funciones a trozos? Aquí tienes algunos recursos, y no dudes en consultar los enlaces para refrescar tus conocimientos sobre algunas de las gráficas más utilizadas:

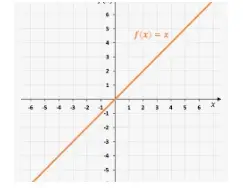
• Funciones lineales como f(x) = 3x -1, y = 4x, y más.
• Funciones cuadráticas como y = -3x2 + 4x, f(x) = 2x2 - 1, y más.
• Funciones cúbicas como f(x) = 4x3 + 1, y = -x3-1, y más.

Vídeos de Funcion a trozos