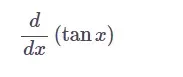Derivada tangente

La derivada o diferenciación de la función tan con respecto a una variable es igual al cuadrado de la función secante.

Si se toma como variable, entonces la función tangente se escribe como tanx en matemáticas. La derivada de la función tan con respecto a x se escribe matemáticamente en el cálculo diferencial como sigue:

En el cálculo, aprendemos que la recta tangente de una función se puede encontrar calculando la derivada. Así que hay una estrecha relación entre las derivadas y las rectas tangentes. Sin embargo, no son lo mismo. Para empezar, la derivada f '(x) es una función, mientras que la recta tangente es, bueno, una recta.

En cambio, la afirmación correcta es ésta "La derivada mide la pendiente de las líneas tangentes".

Piensa en esto: un reloj no es lo mismo que el tiempo. Pero si quieres saber la hora del día, puedes ir a mirar un reloj para averiguarlo. Un reloj mide la hora en cualquier punto del día.

¿Qué es una recta tangente?

Una recta tangente a una función f(x) en un punto dado x = a es una recta (función lineal) que se encuentra con la gráfica de la función en x = a y tiene la misma pendiente que la curva en ese punto.

A veces podemos decir que una recta tangente "sólo toca" la curva, o que "cruza la curva una sola vez "f , pero esas ideas a veces pueden llevarnos por el camino equivocado.

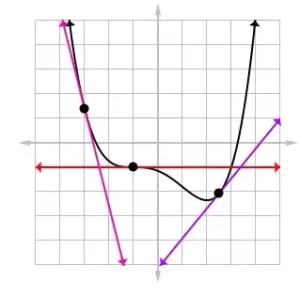
La siguiente gráfica muestra las líneas tangentes (en rojo, morado y magenta) en tres puntos diferentes de una curva y = f(x) (en negro).

Pendiente y derivadas

Entonces, ¿cómo sabemos cuál debe ser la pendiente de la recta tangente? Después de aprender sobre las derivadas, puedes utilizar la sencilla fórmula

m = f '(a).

En esta fórmula, se dan la función f y el valor de x a. Tu trabajo consiste en encontrar m, que representa la pendiente de la recta tangente. Una vez que tengas la pendiente, escribir la ecuación de la recta tangente es bastante sencillo.

Encontrar la recta tangente

Supongamos que se nos pide que encontremos la recta tangente de una función f(x) en un punto dado x = a. A continuación se presenta una aproximación paso a paso:

• Encuentra la derivada, f '(x).
• Introduce x = a para obtener la pendiente. Es decir, calcula m = f '(a).
• Si no está dada en el problema, encuentra la coordenada y del punto. Como siempre, introduce el valor de x en la función para obtener el valor de y. Sea b = f(a).
• Utiliza la forma punto-pendiente y resuelve para y para encontrar la ecuación de la recta tangente. En otras palabras, introduce los valores de m, a y b en la ecuación,
  y = m(x - a) + b.

La derivada mide la pendiente

Volvamos a ver el primer paso, "Encontrar la derivada". Recuerda que la derivada es una función (de la variable de entrada x). Al introducir diferentes valores de entrada, x = a, los valores de salida de f '(x) te dan las pendientes de las líneas tangentes en cada punto x = a.

A esto nos referimos cuando decimos que "la derivada mide la pendiente de las rectas tangentes".

Si quiero saber la pendiente de f en x = 1, entonces calculo f '(1). Y si quiero conocer la pendiente en x = -352/13, entonces calculo f '(-352/13).

Vídeos de Derivada tangente