Función cúbica
Una función cúbica es un polinomio de grado tres.
Por ejemplo, y = x3 + 3x2 - 2x + 5
Las gráficas cúbicas se pueden dibujar encontrando los interceptos de x e y.
Como las gráficas cúbicas no tienen ejes de simetría, los puntos de inflexión deben encontrarse utilizando el cálculo.
Método 1: Factorización
Si la ecuación es de la forma y = (x - a)(x - b)(x - c) se debe utilizar el siguiente método:
Paso 1: Hallar los intersticios de x poniendo y = 0.
Paso 2: Encuentra la intersección de y poniendo x = 0.
Paso 3: Traza los puntos anteriores para dibujar la curva cúbica.
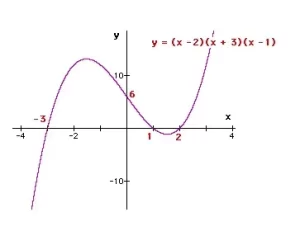
Por ejemplo, dibujar la gráfica de y = (x - 2)(x + 3)(x - 1)
Paso 1:
Encuentra las intersecciones de las x poniendo y = 0.
0 = (x - 2)(x + 3)(x - 1)
x = 2 o -3 o 1
Paso 2:
Encuentra las intersecciones de y poniendo x = 0.
y = (0 - 2)(0 + 3)(0 - 1)
y = -2 x 3 x -1
y = 6
Paso 3:
Traza los puntos y dibuja la curva.
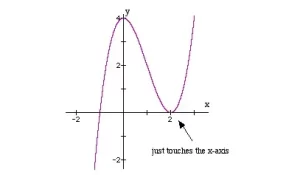
Nota: Las funciones con un factor repetido tienen una gráfica que apenas toca el eje x. Por ejemplo, y = (x - 2)2(x + 1).
Método 2: Transformación
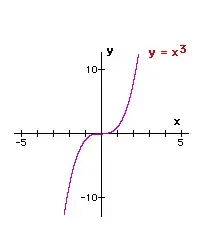
La gráfica de la cúbica básica y = x3 se muestra en el diagrama.
Esta cúbica básica se mueve o transforma de la siguiente manera:
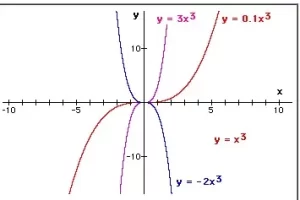
y = ax3 La a tiene el efecto de cambiar la cúbica básica en la dirección y-.
Afecta a la inclinación de la gráfica.
Si a es grande, la cúbica es más empinada.
Si a es pequeño, la cúbica es más plana.
Si a es negativo, la cúbica se invierte.
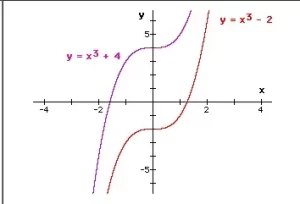
y = x3 + k
La k tiene el efecto de mover la cúbica hacia arriba o hacia abajo del eje y en k unidades.
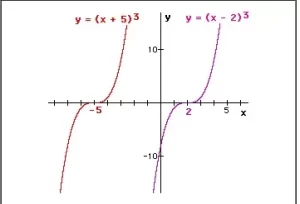
y = (x - h)3
La h tiene el efecto de desplazar la cúbica básica a lo largo del eje x en h unidades.
Vídeos de Función cúbica
https://www.youtube.com/watch?v=qK2QJNptAb8
Entradas Relacionadas
Contenido