Propiedades del arcocoseno

A continuación se presentan algunas propiedades/fórmulas del arcocoseno. Estas son muy útiles para resolver los problemas relacionados con el cos inverso en trigonometría.

• cos(cos-1x) = x sólo cuando x ∈ [-1, 1]
• ([Cuando x ∉ [-1, 1], cos(cos-1x) NO está definido)
• cos-1(cos x) = x, sólo cuando x ∈ [0, π]
• (Cuando x ∉ [0, π], encuentra el ángulo coterminal de x, o aplica las identidades trigonométricas para encontrar el ángulo equivalente de x que se encuentra en [0, π] )
• cos-1(-x) = π - cos-1x
• cos-1(1/x) = sec-1x, cuando |x| ≥ 1
• sin-1x + cos-1x = π/2, cuando x ∈ [-1, 1]

Derivada de Arcos x

Vamos a encontrar la derivada de y = cos-1x. Por la definición de arcocoseno, y = cos-1x puede escribirse como cos y = x. Diferenciando esto en ambos lados con respecto a x usando la regla de la cadena,

- sin y (dy/dx) = 1

dy/dx = -1/sin y ... (1)

Ahora, tenemos sin2y + cos2y = 1 ⇒ sin2y = 1 - cos2y ⇒ sin y = √(1 - cos²y) = √1 - x².

Sustituyendo esto en (1),

dy/dx = -1/√1 - x²

Así, la derivada del arcocos (o) la derivada del cos-1x es -1/√(1 - x²).

Integral de Arcos x

Encontraremos ∫cos-1x dx utilizando la integración por partes. Para ello, escribimos la integral anterior como

∫cos-1x - 1 dx

Usando LIATE, f(x) = cos-1x y g(x) = 1.

Por integración por partes

∫f(x) . g(x) dx = f(x) ∫g(x) dx - ∫(f′(x) ∫g(x) dx) dx + C

∫cos-1x - 1 dx = cos-1x ∫1 dx - ∫ [d/dx(cos-1x) ∫x dx] + C

∫cos-1x dx = cos-1x (x) - ∫ [-1/√1 - x²] x dx + C

Evaluaremos esta integral utilizando la sustitución en u. Para ello, dejemos que 1-x2 = u. Entonces -2x dx = du (o) x dx = -1/2 du.

∫cos-1x dx = x cos-1x - ∫(-1/√u) (-1/2) du + C

= x cos-1x - 1/2 ∫u-1/2 du + C

= x cos-1x - (1/2) (u1/2/(1/2)) + C

= x cos-1x - √u + C

= x cos-1x - √1 - x² + C

Por tanto, ∫cos-1x dx = x cos-1x - √(1 - x²) + C.

Notas importantes sobre el arcocoseno:

Aquí hay algunos puntos importantes a tener en cuenta relacionados con la función arcocoseno.

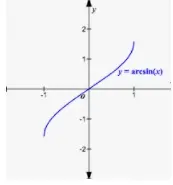
• el arcocoseno puede escribirse como cos-1 (o) arccos (o) acos y es una función con dominio [-1, 1] y rango [0, π].
• El arcocoseno NO es lo mismo que (cos x)-1 ya que (cos x)-1 = 1/(cos x) = sec x.
• cos-1(-x) NO es -cos-1(x), sino que cos-1(-x) = π - cos-1x.
• cos(cos-1x) NO es siempre x. cos(cos-1x) = x sólo cuando x ∈ [-1, 1].
• cos-1(cos x) NO es siempre x. cos-1(cos x) = x sólo cuando x ∈ [0, π].

Vídeos de Gráfica arcocoseno

https://www.youtube.com/watch?v=vJnn6Cjzx_s