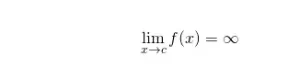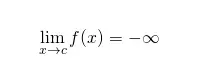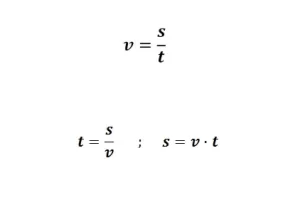Límites al infinito
Por otro lado, decimos que f se aproxima a -∞ a medida que x se aproxima a c si los valores de f(x) se vuelven no acotados en el sentido negativo (valores negativos cada vez mayores) a medida que x se aproxima a c. La notación es similar.
En cualquiera de las dos situaciones, se dice que la función tiene un límite infinito en el número x = c.
La presencia de un límite infinito en una función indica en realidad que la función "explota". Es posible que hayas oído que nada puede viajar más rápido que la velocidad de la luz. Pues bien, esto es cierto en parte porque la función que mide la masa y la energía de un objeto con respecto a su velocidad v tiene un límite infinito en el número v = c, ¡donde c en este caso es la velocidad de la luz! El límite infinito nos dice que la masa/energía se vuelve realmente ilimitada a medida que la velocidad se acerca a c; por lo tanto, ningún objeto físico puede alcanzar esa velocidad.
Un caso de estudio: 1/x
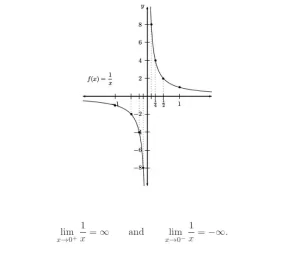
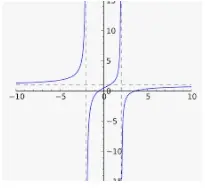
Considera la función f(x) = 1/x. ¿Qué ocurre con los valores de y cuando x se acerca a 0? La gráfica muestra una asíntota vertical en x = 0, lo que es un buen indicio de que se trata de un límite infinito. La función parece salir disparada de la parte superior de la gráfica cuando x se acerca a 0 por la derecha; eso significa que el límite de f es ∞ cuando x → 0 por la derecha. La gráfica cae de la parte inferior de la gráfica cuando x se acerca a 0 desde la izquierda, por lo que el límite de f es -∞ cuando x → 0 desde la izquierda.
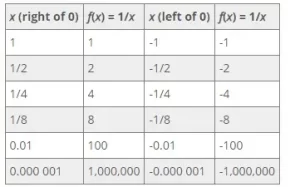
Construyamos una tabla de valores para ilustrar este comportamiento de forma más concreta.
Fíjate en que los valores Y de la segunda columna siguen aumentando sin límite (100; 1.000.000; etc.), y los valores Y de la cuarta columna disminuyen sin límite (-100; -1.000.000; etc.). Algunos de los puntos de la tabla están representados en el gráfico de la ilustración. Traza con tu dedo el gráfico a partir del punto (1,1). Al trazar hacia la izquierda, manteniéndose siempre en el gráfico, acabas llegando a la parte superior. En realidad, la gráfica va hacia arriba más allá de lo que se muestra, ¡y nunca se detiene! Esta es la esencia de un límite infinito.
Según la tabla (o la gráfica), concluimos que: