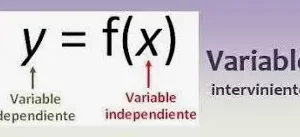
Función racional

Cualquier fracción no está definida cuando su denominador es igual a 0. Este es el punto clave que se utiliza para encontrar el dominio y el rango de una función racional.

Dominio de la función racional

El dominio de una función racional es el conjunto de todos los valores de x que puede tomar la función. Para encontrar el dominio de una función racional y = f(x):

Fijar el denominador ≠ 0 y resolverlo para x.

El conjunto de todos los números reales distintos de los valores de x mencionados en el último paso es el dominio.

Ejemplo: Encontrar el dominio de f(x) = (2x + 1) / (3x - 2).

Solución:

Ponemos el denominador no igual a cero.

3x - 2 ≠ 0
x ≠ 2/3

Así, el dominio = {x ∈ R | x ≠ 2/3}

Rango de la función racional

El rango de una función racional es el conjunto de todas las salidas (valores de y) que produce. Para encontrar el rango de una función racional y= f(x):

Si tenemos f(x) en la ecuación, sustitúyela por y.
Resolver la ecuación para x.
Poner el denominador de la ecuación resultante ≠ 0 y resolverla para y.
El conjunto de todos los números reales distintos de los valores de y mencionados en el último paso es el rango.

Ejemplo: Encontrar el rango de f(x) = (2x + 1) / (3x - 2).

Solución:

Sustituyamos f(x) por y. Entonces y = (2x + 1) / (3x - 2). Ahora, resolveremos esto para x.

(3x - 2) y = (2x + 1)
3xy - 2y = 2x + 1
3xy - 2x = 2y + 1
x (3y - 2) = (2y + 1)
x = (2y + 1) / (3y - 2)

Ahora (3y - 2) ≠ 0
y ≠ 2/3

Así que el rango = {y ∈ R | y ≠ 2/3}

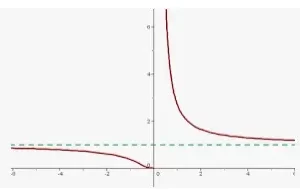
Asíntotas de una función racional

Una función racional puede tener tres tipos de asíntotas: horizontales, verticales y oblicuas. Además de éstas, también puede tener agujeros. Veamos cómo encontrar cada uno de ellos.

Agujeros de una función racional

Los agujeros de una función racional son puntos que parecen estar presentes en la gráfica de la función racional pero que en realidad no lo están. Se pueden obtener fijando los factores lineales que son factores comunes del numerador y del denominador de la función iguales a cero y resolviendo para x. Podemos encontrar las correspondientes coordenadas y de los puntos sustituyendo los valores de x en la función simplificada. Toda función racional NO necesita tener agujeros. Los agujeros sólo existen cuando el numerador y el denominador tienen factores comunes lineales.

Ejemplo: Encuentra los huecos de la función f(x) = (x2 + 5x + 6) / (x2 + x - 2).

Solución:

Factoricemos el numerador y el denominador y veamos si hay factores comunes.

f(x) = [ (x + 2)(x + 3) ] / [ (x + 2) (x - 1) ] = [ ̶(̶x̶ ̶+̶ ̶2̶)̶(x + 3) ] / [ ̶(̶x̶ ̶+̶ ̶2̶)̶ (x - 1) ] = (x + 3) / (x - 1)

Como (x + 2) se ha eliminado, hay un agujero en x = -2. Su coordenada y es f(-2) = (-2 + 3) / (-2 - 1) = -1/3.

Por lo tanto, hay un agujero en (-2, -1/3).

Asíntota vertical de una función racional

Una asíntota vertical (VA) de una función es una línea vertical imaginaria a la que su gráfica parece estar muy cerca, pero nunca se toca. Es de la forma x = algún número. Aquí, "algún número" está estrechamente relacionado con los valores excluidos del dominio. Pero hay que tener en cuenta que no puede haber una asíntota vertical en x = algún número si hay un agujero en el mismo número. Una función racional puede tener una o más asíntotas verticales. Así que para encontrar las asíntotas verticales de una función racional

Simplifica primero la función para cancelar todos los factores comunes (si los hay).
Poner el denominador = 0 y resolver para (x) (o equivalentemente sólo obtener los valores excluidos del dominio evitando los agujeros).

Asíntota horizontal de una función racional

Una asíntota horizontal (HA) de una función es una línea horizontal imaginaria a la que su gráfica parece estar muy cerca pero nunca se toca. Es de la forma y = algún número. Aquí, "algún número" está estrechamente relacionado con los valores excluidos del rango. Una función racional puede tener como máximo una asíntota horizontal. Una forma fácil de encontrar la asíntota horizontal de una función racional es utilizar los grados del numerador (N) y de los denominadores (D).

Si N < D, entonces hay una HA en y = 0.
Si N > D, entonces no hay HA.
Si N = D, entonces la HA es y = razón de los coeficientes principales.

Asíntotas oblicuas de una función racional

Una asíntota oblicua es también una línea oblicua imaginaria a la que parece tocar una parte de la gráfica. Una función racional tiene una asíntota oblicua sólo cuando el grado del numerador (N) es exactamente uno mayor que el grado del denominador (D). Su ecuación es y = cociente que se obtiene dividiendo el numerador entre el denominador mediante la división larga.

Graficar funciones racionales

Estos son los pasos para graficar una función racional:

• Identificar y dibujar la asíntota vertical utilizando una línea de puntos.
• Identifica y dibuja la asíntota horizontal utilizando una línea de puntos.
• Trazar los huecos (si los hay)
• Encuentra la intersección x (utilizando y = 0) y la intersección y (utilizando x = 0) y traza las mismas.
• Dibuja una tabla de dos columnas x e y y coloca las intersecciones x y las asíntotas verticales en la tabla. A continuación, toma algunos números al azar en la columna x a cada lado de cada una de las intersecciones x y asíntotas verticales.
• Calcula los valores y correspondientes sustituyendo cada uno de ellos en la función.
• Traza todos los puntos de la tabla y une las curvas sin tocar las asíntotas.

Vídeos de Función racional