Métodos para sumar vectores

Los vectores tienen magnitud y dirección, no se puede simplemente sumar dos vectores para obtener su suma. La suma de vectores no es tan sencilla como la suma de escalares. Para entenderlo mejor, consideremos el ejemplo de un coche que recorre 16 kilómetros al norte y 16 kilómetros al sur. Aquí, la distancia total recorrida es de 20 millas pero el desplazamiento es cero. Los desplazamientos al Norte y al Sur son cantidades vectoriales, y las direcciones opuestas hacen que los desplazamientos individuales se cancelen entre sí.

Suma de vectores

Como ya hemos comentado, los vectores no se pueden sumar simplemente de forma algebraica. A continuación se indican algunos puntos que hay que recordar al sumar vectores:

• Los vectores se suman geométricamente y no algebraicamente.
• Los vectores cuya resultante hay que calcular se comportan de forma independiente.
• La suma de vectores no es otra cosa que encontrar la resultante de un número de vectores que actúan sobre un cuerpo.
• La suma de vectores es conmutativa. Esto significa que el vector resultante es independiente del orden de los vectores.

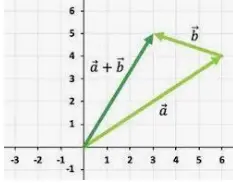
Ley del triángulo de la adición de vectores

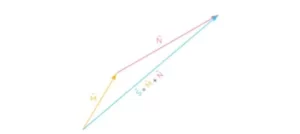
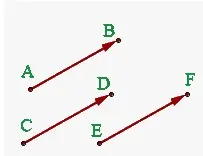
La famosa ley del triángulo puede utilizarse para la suma de vectores y este método también se denomina método de la cabeza a la cola. Según esta ley, se pueden sumar dos vectores colocándolos juntos de forma que la cabeza del primer vector se una a la cola del segundo. Así, uniendo la cola del primer vector con la cabeza del segundo, podemos obtener la suma de vectores resultante. La suma de vectores utilizando la ley del triángulo puede ser con los siguientes pasos:

En primer lugar, se colocan los dos vectores M y N de forma que la cabeza del vector M conecte con la cola del vector N.
Y luego, para hallar la suma, se dibuja un vector resultante S de manera que conecte la cola de M con la cabeza de N.
Por lo tanto, matemáticamente, la suma o la resultante, el vector S, en la imagen de abajo puede expresarse como S = M + N.

Así, cuando se suman los dos vectores M y N utilizando la ley del triángulo, podemos ver que se forma un triángulo con los dos vectores originales M y N, y el vector suma S.

En la figura anterior, utilizando la ley del triángulo, podemos concluir lo siguiente

OP + PR = O

OP + OQ = OR, ya que PR = OQ

Por lo tanto, podemos concluir que las leyes del triángulo de la adición de vectores y la ley del paralelogramo de la adición de vectores son equivalentes entre sí.

Vídeos de Métodos para sumar vectores