Movimiento circular
El movimiento circular es el movimiento de un cuerpo que sigue una trayectoria circular. El movimiento circular uniforme es un tipo específico de movimiento circular en el que el movimiento de un cuerpo que sigue una trayectoria circular es de velocidad constante. El cuerpo tiene un punto central fijo y permanece equidistante de él en cualquier posición.
Cuando un objeto gira en círculo, la descripción de su movimiento se vuelve interesante en muchos sentidos. Para entender mejor el movimiento circular veamos un ejemplo.
Supongamos que tenemos una pelota atada a una cuerda y la movemos constantemente con un movimiento circular. Entonces observamos dos cosas:
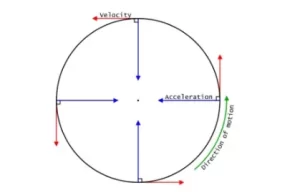
La velocidad de la pelota es constante. Traza un círculo con un centro fijo.
En cada punto de su movimiento, la pelota cambia de dirección. Por lo tanto, podemos decir que para mantenerse en una trayectoria circular, la pelota tiene que cambiar su dirección continuamente.
Del segundo punto se desprende un resultado importante. La primera ley del movimiento de Newton nos dice que no puede haber aceleración sin una fuerza neta. Por tanto, debe haber una fuerza asociada al movimiento circular. En otras palabras, para que se produzca el movimiento circular tiene que actuar una fuerza neta sobre el objeto. Así, el cambio de dirección es el resultado de una fuerza centrípeta.
La fuerza centrípeta es la fuerza que actúa sobre un cuerpo en una trayectoria circular. Apunta hacia el centro alrededor del cual se mueve el cuerpo.
Mientras la pelota esté unida a la cuerda, seguirá la trayectoria circular. En el momento en que la cuerda se rompe o se suelta, la fuerza centrípeta deja de actuar y la pelota sale volando.
Terminología del movimiento circular uniforme
Para estudiar el movimiento circular uniforme, definimos los siguientes términos.
Periodo de tiempo (T)
El periodo de tiempo (T) es el tiempo que tarda la bola en completar una revolución. Se denomina "T". Si 'r' es el radio del círculo de movimiento, entonces en el tiempo 'T' nuestra pelota cubre una distancia = 2πr. Supongamos que la pelota tarda 3 segundos en completar una revolución. Entonces T= 3 segundos.
Frecuencia (f)
El número de revoluciones que nuestra pelota completa en un segundo es la frecuencia de la revolución. Denotamos la frecuencia por f y f = 1/T. La unidad de la frecuencia es el Hertz (Hz). Un Hz significa una revolución por segundo. Aquí la frecuencia será de 1/3 Hz.
Fuerza centrípeta
Hemos visto antes que un cuerpo que se mueve en un círculo cambia su dirección continuamente. Por lo tanto, dijimos que el movimiento circular es un movimiento acelerado. Por las leyes de Newton, sabemos que un cuerpo puede acelerar sólo cuando actúa sobre él alguna fuerza.
En el caso del movimiento circular, esta fuerza es la fuerza centrípeta. Si "m" es la masa del cuerpo, entonces la fuerza centrípeta sobre él viene dada por F = mv2/r; donde "r" es el radio de la órbita circular.
Velocidad angular
También podemos hacernos una idea de la velocidad con la que un objeto se mueve en un círculo si sabemos a qué velocidad gira la línea que une el objeto con el centro del círculo. Esto se mide midiendo la velocidad con la que cambia el ángulo subtendido en el centro. Esta cantidad es ω y ω = Cambio de ángulo por unidad de tiempo. Por lo tanto, ω es la velocidad angular.
La unidad del SI es el radián / s o rad/s. Para una sola rotación, el cambio de ángulo es 2π y el tiempo empleado es 'T', por lo tanto podemos escribir
ω = 2π/T = 2πν ...(4)
Se suele medir en r.p.m o rotaciones por minuto. ω = 1 r.p.m, si un cuerpo completa una rotación por minuto. También podemos convertir r.p.m a radianes por segundo como i r.p.m. = 2π/60s = π/30 rad/s
Vídeos de movimiento circular