Relaciones trigonometricas
Las identidades trigonométricas son ecuaciones que se relacionan con diferentes funciones trigonométricas y son verdaderas para cualquier valor de la variable que esté en el dominio. Básicamente, una identidad es una ecuación que se cumple para todos los valores de la(s) variable(s) presentes en ella.
Por ejemplo, algunas de las identidades algebraicas son
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab+ b2
(a + b)(a-b)= a2 - b2
Las identidades algebraicas sólo relacionan las variables mientras que las identidades trigonométricas relacionan las 6 funciones trigonométricas seno, coseno, tangente, cosecante, secante y cotangente.
Identidades trigonométricas recíprocas
Ya sabemos que los recíprocos de seno, coseno y tangente son cosecante, secante y cotangente respectivamente.
Por lo tanto, las identidades recíprocas se dan como
sen θ = 1/cosecθ (O) cosec θ = 1/sinθ
cos θ = 1/secθ (O) sec θ = 1/cosθ
tan θ = 1/cotθ (O) cot θ = 1/tanθ
Identidades trigonométricas pitagóricas
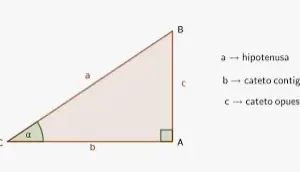
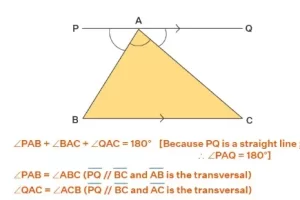
Las identidades trigonométricas pitagóricas en trigonometría se derivan del teorema de Pitágoras. Aplicando el teorema de Pitágoras al triángulo rectángulo de abajo, obtenemos
Opuesto2 + Adyacente2 = Hipotenusa2
Dividiendo ambos lados por Hipotenusa2
Opuesto2/Hipotenusa2 + Adyacente2/Hipotenusa2 = Hipotenusa2/Hipotenusa2
sin2θ + cos2θ = 1
Esta es una de las identidades pitagóricas. Del mismo modo, podemos derivar otras dos identidades trigonométricas pitagóricas.
1 + tan2θ = sec2θ
1 + cot2θ = cosec2θ
Identidades trigonométricas complementarias y suplementarias
Los ángulos complementarios son un par de dos ángulos tales que su suma es igual a 90°. El complemento de un ángulo θ es (90 - θ). Las razones trigonométricas de los ángulos complementarios son
sin (90°- θ) = cos θ
cos (90°- θ) = sin θ
cosec (90°- θ) = sec θ
sec (90°- θ) = cosec θ
tan (90°- θ) = cot θ
cot (90°- θ) = tan θ
Los ángulos suplementarios son un par de dos ángulos tales que su suma es igual a 180°. El suplemento de un ángulo θ es (180 - θ). Las razones trigonométricas de los ángulos suplementarios son
sin (180°- θ) = sinθ
cos (180°- θ) = -cos θ
cosec (180°- θ) = cosec θ
sec (180°- θ)= -sec θ
tan (180°- θ) = -tan θ
cot (180°- θ) = -cot θ
Identidades trigonométricas de suma y diferencia
Las identidades de suma y diferencia incluyen las fórmulas de sen(A+B), cos(A-B), cot(A+B), etc.
sin (A+B) = sin A cos B + cos A sin B
sin (A-B) = sin A cos B - cos A sin B
cos (A+B) = cos A cos B - sin A sin B
cos (A-B) = cos A cos B + sin A sin B
tan (A+B) = (tan A + tan B)/(1 - tan A tan B)
tan (A-B) = (tan A - tan B)/(1 + tan A tan B)