Trapecio isósceles

Las propiedades del trapecio son las siguientes:

• Las bases son paralelas por definición.
• Cada ángulo de la base inferior es suplementario al ángulo de la base superior del mismo lado.
• Las propiedades del trapecio isósceles son las siguientes:
• Las propiedades de un trapecio se aplican por definición (bases paralelas).
• Los catetos son congruentes por definición.
• Los ángulos de la base inferior son congruentes.
• Los ángulos de la base superior son congruentes.
• Cualquier ángulo de la base inferior es suplementario a cualquier ángulo de la base superior.
• Las diagonales son congruentes.
• Los ángulos suplementarios pueden ser la propiedad más difícil de detectar en los diagramas anteriores. Debido a los lados paralelos, los ángulos consecutivos son ángulos interiores del mismo lado y por lo tanto son suplementarios. (Por cierto, todos los cuadriláteros especiales, excepto la cometa, contienen ángulos suplementarios consecutivos).

Como cuadrilátero, el trapecio es una forma de cuatro lados. La primera propiedad única del trapecio es que sólo tiene un par de lados paralelos. El trapezoide también se denomina a veces trapecio. Los trapezoides tienen a veces diferentes longitudes de lado y diferentes medidas de ángulo, pero todos los ángulos suman 360 grados como en cualquier cuadrilátero.

Definición de un Trapecio Isósceles

¿Qué tiene de especial el trapecio isósceles? Bueno, si recuerdas, un triángulo isósceles tiene dos ángulos de base que son congruentes y dos catetos que son congruentes. El trapecio isósceles obtiene sus propiedades a partir de una combinación de estos elementos. Un trapecio isósceles es un cuadrilátero que tiene las siguientes propiedades:

• Un par de lados paralelos (AB y DC)
• Un par de catetos congruentes (DA y CB)
• Los ángulos de las bases son congruentes (m<D = m<C)
• Las diagonales son congruentes (AC y BD)
• Los ángulos opuestos son suplementarios (su suma es de 180 grados)
• m<A + m<C = 180; m<B + m<D = 180

Trapecio Isósceles

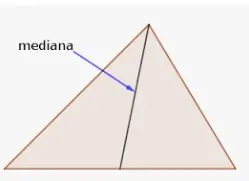
La mediana de un trapecio isósceles es el segmento de recta que se forma cuando unimos el punto medio de un cateto con el punto medio del otro cateto de un trapecio isósceles. La mediana forma un teorema especial sólo para los trapecios isósceles. La longitud de la mediana es la mitad de la suma de los dos lados paralelos. Si asignamos las variables a y b a la medida de los lados paralelos, entonces la longitud de la mediana es (a + b)/ 2.

La mediana también es paralela a los dos lados paralelos. El segmento de recta MN es paralelo a los segmentos de recta AB y DC.

Mediana del trapecio
Veamos un ejemplo:

Si a =12 cm y b =14 cm,

entonces MN = (12 + 14)/2

MN = 26/2 = 13 cm

Vídeos de Trapecio isósceles

https://www.youtube.com/watch?v=8uvGfq23IW4