Volumen geometria
La geometría es una rama de las matemáticas que se ocupa de la forma, el tamaño, la posición relativa de las figuras y las propiedades de las formas. Surge de forma independiente en varias culturas primitivas como una forma práctica de tratar las longitudes, el área y los volúmenes. La geometría puede dividirse en dos tipos diferentes: La Geometría Plana y la Geometría Sólida. La Geometría Plana se ocupa de formas como círculos, triángulos, rectángulos, cuadrados y otras. Mientras que la Geometría Sólida se ocupa de calcular la longitud, el perímetro, el área y el volumen de diversas figuras y formas geométricas.
Volumen geometría
La principal preocupación de todo estudiante sobre la asignatura de matemáticas son las fórmulas de geometría. Se utilizan para calcular la longitud, el perímetro, el área y el volumen de diversas formas y figuras geométricas. Hay muchas fórmulas geométricas, que están relacionadas con la altura, la anchura, la longitud, el radio, el perímetro, el área, la superficie o el volumen y mucho más. Algunas fórmulas geométricas son bastante complicadas y es posible que apenas las veas, sin embargo, hay algunas fórmulas básicas que se usan en nuestra vida diaria para calcular la longitud, el espacio, etc.
Fórmulas básicas de geometría
- Perímetro de un cuadrado = P = 4a
Donde a = Longitud de los lados de un cuadrado - Perímetro de un Rectángulo = P = 2(l+b)
Donde, l = Longitud; b = Anchura - Área de un cuadrado = A = a2
Donde a = Longitud de los lados del cuadrado - Área de un rectángulo = A = l×b
Donde, l = Longitud; b = Anchura - Área de un triángulo = A = ½×b×h
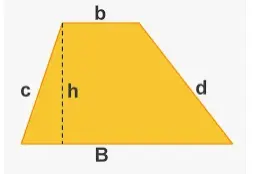
Donde, b = base del triángulo; h = altura del triángulo - Área de un trapecio = A = ½×(b1 + b2)×h
Donde b1 y b2 son las bases del trapecio; h = altura del trapecio - Área de un círculo = A = π×r2
Circunferencia de un círculo = A = 2πr
Donde, r = Radio del Círculo - Superficie de un cubo = S = 6a2
Donde, a = Longitud de las caras de un Cubo - Superficie curva de un Cilindro = 2πrh
Superficie total de un Cilindro = 2πr(r + h)
Volumen de un cilindro = V = πr2h
Donde, r = Radio de la base del Cilindro; h = Altura del Cilindro - Superficie curva de un cono = πrl
Superficie total de un cono = πr(r+l) = πr[r+√(h2+r2)] Volumen de un cono = V = ⅓×πr2h
Donde, r = Radio de la base del Cono, h = Altura del Cono - Superficie de una esfera = S = 4πr2
Volumen de una esfera = V = 4/3×πr3
Donde, r = Radio de la Esfera
Vídeos de Volumen geometría
Entradas Relacionadas
Contenido