Rombo

El rombo es un caso especial del paralelogramo y es un cuadrilátero de cuatro lados. En un rombo, los lados opuestos son paralelos y los ángulos opuestos son iguales. Además, todos los lados de un rombo tienen la misma longitud y las diagonales se bisecan entre sí en ángulo recto. El rombo también se denomina diamante o romboide. La forma plural de rombo es rombo o rombos.

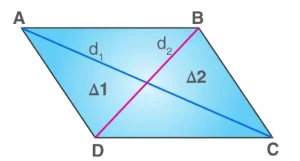
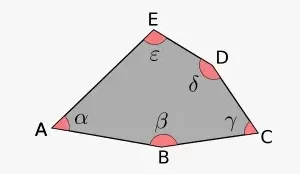
En la figura anterior, puedes ver un rombo ABCD, donde AB, BC, CD y AD son los lados de un rombo y AC y BD son las diagonales de un rombo.

¿Es el cuadrado un rombo?

El rombo tiene todos sus lados iguales, al igual que el cuadrado. Además, las diagonales del cuadrado son perpendiculares entre sí y bisecan los ángulos opuestos. Por tanto, un cuadrado es un tipo de rombo.

Ángulos del rombo

A continuación se presentan algunos datos importantes sobre los ángulos del rombo:

• El rombo tiene cuatro ángulos interiores.
• La suma de los ángulos interiores de un rombo suma 360 grados.
• Los ángulos opuestos de un rombo son iguales entre sí.
• Los ángulos adyacentes son complementarios.
• En un rombo, las diagonales se bisecan entre sí en ángulo recto.
• Las diagonales de un rombo bisecan estos ángulos.

Área del rombo

El área del rombo es la región cubierta por él en un plano bidimensional. La fórmula del área es igual al producto de las diagonales del rombo dividido por 2. Se puede representar como

• Área del rombo, A = (d1 x d2)/2 unidades cuadradas
  donde d1 y d2 son las diagonales de un rombo.

Perímetro del rombo

El perímetro de un rombo es la longitud total de sus límites. O podemos decir que la suma de los cuatro lados de un rombo es su perímetro. La fórmula de su perímetro viene dada por:

• El perímetro del rombo, P = 4a unidades
  Donde las diagonales del rombo son d1 y d2 y "a" es el lado.

Propiedades del rombo

Algunas de las propiedades importantes del rombo son las siguientes:

• Todos los lados del rombo son iguales.
• Los lados opuestos de un rombo son paralelos.
• Los ángulos opuestos de un rombo son iguales.
• En un rombo, las diagonales se bisecan entre sí en ángulos rectos.
• Las diagonales bisecan los ángulos de un rombo.
• La suma de dos ángulos adyacentes es igual a 180 grados.
• Las dos diagonales de un rombo forman cuatro triángulos rectángulos que son congruentes entre sí
• Obtendrás un rectángulo al unir el punto medio de los lados.
• Obtendrás otro rombo al unir los puntos medios de la mitad de la diagonal.
• Alrededor de un rombo no puede haber ninguna circunferencia que lo circunscriba.
• Dentro de un rombo no puede haber ninguna circunferencia inscrita.
• Se obtendrá un rectángulo, en el que se unen los puntos medios de los 4 lados, y la longitud y la anchura del rectángulo serán la mitad del valor de la diagonal principal, de modo que el área del rectángulo será la mitad del rombo.
• Cuando la diagonal más corta es igual a uno de los lados de un rombo, se forman dos triángulos equiláteros congruentes.
• Se obtendrá una superficie cilíndrica que tiene un cono convexo en un extremo y un cono cóncavo en el otro extremo cuando el rombo gira alrededor de un lado cualquiera como eje de rotación.
• Obtendremos una superficie cilíndrica con conos cóncavos en ambos extremos cuando el rombo gire en torno a la línea que une los puntos medios de los lados opuestos como eje de rotación.
• Se obtendrá un sólido con dos conos unidos a sus bases cuando el rombo gire en torno a la diagonal más larga como eje de rotación. En este caso, el diámetro máximo del sólido es igual a la diagonal más corta del rombo.
• Se obtiene un sólido con dos conos unidos a sus bases cuando el rombo gira en torno a la diagonal más corta como eje de rotación. En este caso, el diámetro máximo del sólido es igual a la diagonal más larga del rombo.

Vídeos de Rombo