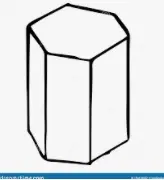
Área de un prisma hexagonal

La superficie de un prisma hexagonal se define como la región total cubierta por las superficies de un prisma hexagonal. Como tiene una base plana, tiene una superficie total y una superficie curva/lateral. Un prisma hexagonal tiene 8 caras, 18 aristas y 12 vértices. Tiene bases superiores e inferiores iguales con diagonales que cruzan el punto central de un hexágono regular.

La superficie de un prisma hexagonal se expresa en unidades cuadradas, siendo las unidades comunes los metros cuadrados, los centímetros cuadrados, las pulgadas cuadradas, etc. Al igual que otras formas tridimensionales, un prisma hexagonal también puede tener dos tipos de áreas,

• Área de superficie total (TSA)
• Área superficial lateral (ASL)

Fórmula del área superficial de un prisma hexagonal

El área superficial de un prisma hexagonal es la suma de las áreas de sus caras y de su base. El área de la superficie de un prisma hexagonal da el área de cada cara del prisma. Si la longitud de la apotema del prisma es "a", la longitud de la base del prisma es "b" y la altura del prisma es "h", el área superficial de un prisma hexagonal viene dada por

• Área superficial total, TSA= 2(área de la base del hexágono) + 6(área de la cara del rectángulo) unidades cuadradas. = 6b(a + h) o 6ah + 3√3a2 (en caso de prisma hexagonal regular)
• Superficie lateral, LSA = Ph = 6(área del rectángulo) = 6ah unidades cuadradas

a = longitud de la base
a = longitud de la apotema
h = altura

En el caso de un prisma hexagonal regular, el Área Superficial Total, AST = 6ah + 3√3a2, donde a = longitud de la base y h= altura del prisma. La fórmula del prisma hexagonal para calcular la superficie sigue siendo la misma para todos los tipos de prismas hexagonales. Los prismas hexagonales pueden ser regulares o irregulares.

• Un prisma hexagonal regular es un prisma hexagonal que tiene como base hexágonos regulares y todas las caras tienen la misma longitud.
• Un prisma hexagonal irregular tiene bases hexagonales irregulares, por lo que las caras de sus bases hexagonales no tienen la misma longitud.

Derivación de la superficie de un prisma hexagonal

Tomemos un prisma hexagonal, que tiene la longitud de la apotema "a", la longitud de la base "b", y la altura "h". Para determinarlo cortamos el prisma hexagonal en su red y lo abrimos. La fórmula general de la superficie lateral de un prisma es el producto de su base por su altura. Así, la superficie lateral de un prisma hexagonal puede darse hallando el perímetro de la base del prisma multiplicado por su altura. Sabemos que la base del prisma hexagonal tiene forma de hexágono.

Superficie lateral de un prisma hexagonal

La superficie lateral del prisma hexagonal es la suma del área de 6 caras rectangulares. Por tanto, el área de la superficie lateral, L = 6ah = 6ah unidades cuadradas

Área superficial total, T = 6(área de la cara del rectángulo) + 2(área de la base del hexágono) unidades cuadradas. = 6ah + 3√3a2

¿Cómo encontrar el área de la superficie de un prisma hexagonal?

Para calcular el área de la superficie de un prisma hexagonal se siguen los siguientes pasos :

• Paso 1: Calcular el área de la base hexagonal utilizando la fórmula, 3√3a2
• Paso 2: Hallar el área de las seis caras rectangulares.
• Paso 3: Sumar todas las áreas para obtener el área total de la superficie de un prisma cuadrado, mientras que el área de las 6 caras rectangulares da el área lateral del prisma cuadrado.

Vídeos de Área de un prisma hexagonal

https://www.youtube.com/watch?v=0F6Gw9D58ls