Mediatriz de un triángulo
Una bisectriz de un ángulo es una línea recta trazada desde el vértice de un triángulo hasta su lado opuesto de forma que divide el ángulo en dos ángulos iguales o congruentes.
Teoremas de la bisectriz del ángulo de los triángulos
Teorema de la bisectriz del ángulo interno
La bisectriz de un ángulo de un triángulo divide el lado opuesto en dos partes proporcionales a los otros dos lados del triángulo.
Teorema de la bisectriz interna de un ángulo
En un triángulo, si el punto interior es equidistante de los dos lados de un triángulo, entonces ese punto se encuentra en la bisectriz del ángulo formado por los dos segmentos de recta.
Teorema del bisector del ángulo externo
La bisectriz externa del ángulo divide externamente el lado opuesto en la proporción de los lados que contienen el ángulo, y esta condición suele darse en triángulos no equiláteros.
Según el teorema de la bisectriz del ángulo, la bisectriz del ángulo de un triángulo divide el lado opuesto en dos partes que son proporcionales a los otros dos lados del triángulo.
Teorema de la bisectriz del ángulo interior
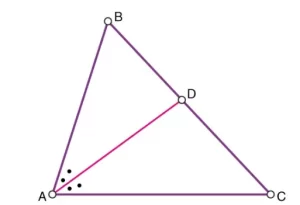
En el triángulo ABC, la bisectriz del ángulo corta el lado BC en el punto D. Véase la figura siguiente.
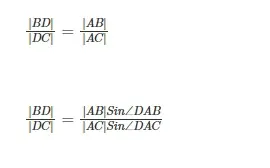
Según el teorema de la bisectriz del ángulo, la razón del segmento de línea BD a DC es igual a la razón de la longitud del lado AB a AC.
A la inversa, cuando un punto D en el lado BC divide a BC en una proporción similar a los lados AC y AB, entonces la bisectriz del ángulo de ∠ A es AD. Por lo tanto, de acuerdo con el teorema, si D se encuentra en el lado BC, entonces,
Si D es exterior al lado BC, se requiere aplicar ángulos dirigidos y segmentos de línea dirigidos en el cálculo.
El teorema del bisector del ángulo se aplica cuando se conocen las longitudes de los lados y los bisectores del ángulo.
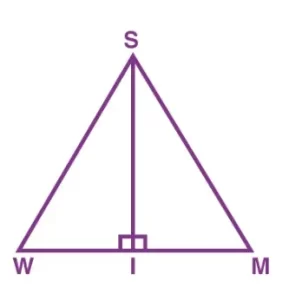
Teorema de la bisectriz perpendicular
Según este teorema, si un punto es equidistante de los puntos extremos de un segmento de recta en un triángulo, entonces está en la bisectriz de la recta.
Alternativamente, podemos decir que la mediatriz divide el segmento de recta dado en dos partes iguales, a las que es perpendicular. En el caso de un triángulo, si se traza una mediatriz desde el vértice hasta el lado opuesto, entonces divide el segmento en dos segmentos congruentes.
Ejemplo resuelto sobre el teorema de la bisectriz del ángulo
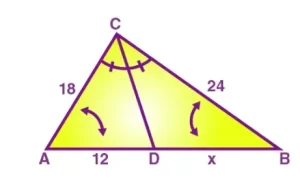
Encuentra el valor de x para el triángulo dado usando el teorema del bisector del ángulo.
Solución:
Dado que
AD = 12, AC = 18, BC=24, DB = x
Según el teorema de la bisectriz del ángulo
AD/AC = DB/BC
Sustituyendo ahora los valores, obtenemos
12/18 = x/24
X = (⅔)24
x = 2(8)
x= 16
Por lo tanto, el valor de x es 16.
Vídeos de Mediatriz de un triángulo
Entradas Relacionadas
Contenido