¿Qué es un poliedro?

Un poliedro es un sólido que está limitado sólo por superficies planas que llamamos caras, las intersecciones de las caras se llaman aristas y los puntos donde se cortan las aristas se llaman esquinas. Las líneas diagonales se llaman líneas que unen esquinas que no pertenecen a la misma cara.

¿Qué es un poliedro regular?

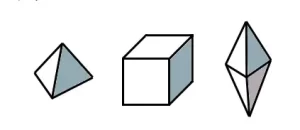
Como puedes imaginar, un poliedro regular es aquel que todas sus caras son polígonos regulares. En total, sólo hay 5 poliedros regulares que ya conoces, cada uno de estos poliedros tiene el prefijo del número de caras.

Poliedros regulares

En un poliedro regular, todos los polígonos que lo componen son especiales: todos son polígonos regulares congruentes. Sólo existen cinco poliedros regulares. Sus nombres y número de caras son los siguientes:

• Un tetraedro tiene cuatro caras.
• El cubo tiene seis caras.
• El octaedro tiene ocho caras.
• El dodecaedro tiene 12 caras.
• El isocaedro tiene 20 caras.

El tetraedro, el octaedro y el icosaedro están formados por triángulos congruentes. El cubo está compuesto por cuadrados congruentes y el dodecaedro por pentágonos regulares.

Esferas

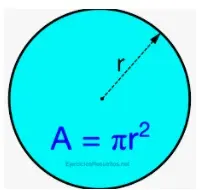
Otra superficie geométrica muy específica es la esfera. Una esfera está formada por todos los puntos que equidistan de un punto fijo determinado en el espacio. Este punto fijo es el centro de la esfera; un segmento con un punto final en el centro y otro en la esfera es un radio. Una esfera es básicamente como un círculo tridimensional. En cierto modo, también es como un poliedro regular con un número infinito de caras, tal que el área de cada cara se aproxima a cero. Este límite, sin embargo, no existe porque el conjunto de poliedros regulares es finito: un poliedro regular no puede tener más de 20 caras.

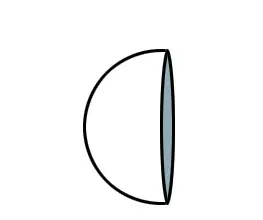
Así como un semicírculo es un arco de 180 grados, o la mitad de un círculo, una semiesfera es la mitad de una esfera.

Las esferas son difíciles de representar Las esferas son difíciles de representar en una pantalla de ordenador bidimensional, así que para intentar visualizar una esfera, lo mejor es estudiar la figura del hemisferio e imaginar dos hemisferios unidos. También hay innumerables ejemplos de esferas o casi esferas en la vida real. Las pelotas de baloncesto y de bolos son esféricas. También lo son la Tierra y los demás planetas de este sistema solar. Por suerte para los estudiantes de geometría, los términos en los que se definen las esferas y las reglas por las que se rigen son sencillos.

Vídeos de Poliedros regulares