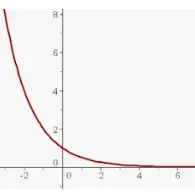
Asíntota vertical

Una asíntota vertical es una línea vertical que parece coincidir con la gráfica de una función, pero que en realidad nunca se encuentra con la curva. La asíntota vertical de una función desempeña un papel importante a la hora de graficar una función.

La asíntota vertical de una función y = f(x) es una recta vertical x = k cuando y→∞ o y→ -∞. Se suele denominar VA. Matemáticamente, si x = k es la VA de una función y = f(x) entonces al menos una de las siguientes afirmaciones es cierta:

lim x→k f(x) = ±∞ (o)
lim x→k₊ f(x) = ±∞ (o)
lim x→k- f(x) = ±∞

Una asíntota vertical es una línea vertical a lo largo de la cual la función se vuelve ilimitada (o bien y tiende a ∞ o a -∞) pero no toca ni cruza la curva. Si x = k es el VA de una función y = f(x) entonces k NO está presente en el dominio de la función. Una función puede tener cualquier número de asíntotas verticales, es decir, puede tener 0, 1, 2, ..., o un número infinito de VAs. Representamos una VA mediante una línea vertical punteada y si el eje y es la VA, entonces normalmente no la mostramos mediante una línea punteada. He aquí algunos ejemplos de asíntotas verticales.

Asíntotas verticales de la gráfica

Al ver los ejemplos anteriores, es posible que ya tengas una idea de cómo determinar las asíntotas verticales de una gráfica. Si una parte de la gráfica se vuelve vertical, entonces es probable que haya una VA a lo largo de esa línea vertical. El valor de la función se convierte en ∞ o -∞ en el valor de x a lo largo del cual has encontrado la VA. Pero ten en cuenta que una asíntota vertical nunca debe tocar la gráfica.

Asíntotas verticales a partir de la ecuación

A partir de la definición de asíntota vertical, si x = k es el VA de una función f(x) entonces lim x→k f(x) = ∞ (o) lim x→k f(x) = -∞. Para identificarlas, basta con pensar qué valores de x harían que el límite de la función fuera ∞ o -∞.

VA de f(x) = 1/(x+1) es x = -1 ya que lim ₓ→₋₁ 1/(x+1) = ∞.
Los VAs de f(x) = 1/[(x+1)(x-2)] son x = -1 y x = 2 ya que los límites izquierdo/derecho en cada uno de x = -1 y x = 2 es ∞ o -∞.

Asíntotas verticales de una función racional

Para encontrar las asíntotas verticales de una función racional no es necesario utilizar el concepto de límite (que es un poco difícil). En su lugar, utilice los siguientes pasos:

• Paso 1: Simplificar la función racional, es decir, factorizar el numerador y el denominador de la función racional y cancelar los factores comunes.
• Paso 2: Establezca el denominador de la función racional simplificada en cero y resuelva.
  Este es un ejemplo para encontrar las asíntotas verticales de una función racional.

Ejemplo: Encontrar las asíntotas verticales de f(x) = (x + 1) / (x2 - 1).

Solución:

Factoricemos y simplifiquemos la expresión dada:

Entonces f(x) = (x + 1) / [ (x + 1) (x - 1) ] = 1 / (x - 1).

Ahora, pon el denominador a cero. Entonces

(x - 1) = 0

x = 1

Así que x = 1 es el VA de f(x).

Vídeos de Asíntota vertical

https://www.youtube.com/watch?v=P7m-u3IuAFY