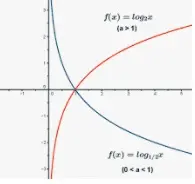
Funcion logaritmica

En matemáticas, la función logarítmica es una función inversa a la exponenciación. La función logarítmica se define como

Para x > 0 , a > 0, y a ≠1

y= loga x si y sólo si x = ay

Entonces la función viene dada por

f(x) = loga x

La base del logaritmo es a. Esto puede leerse como log base a de x. Las 2 bases más comunes utilizadas en las funciones logarítmicas son la base 10 y la base e.

Función logarítmica común

La función logarítmica con base 10 se llama función logarítmica común y se denota por log10 o simplemente log.

f(x) = log10 x

Función logarítmica natural

La función logarítmica de base e se llama función logarítmica natural y se denota por loge.

f(x) = loge x

Propiedades de las funciones logarítmicas

Las funciones logarítmicas tienen algunas propiedades que permiten simplificar los logaritmos cuando la entrada es en forma de producto, cociente o el valor llevado a la potencia. Algunas de las propiedades se enumeran a continuación.

Regla del producto

logb MN = logb M + logb N

Multiplica dos números con la misma base y luego suma los exponentes.

Ejemplo: log 30 + log 2 = log 60

Regla del cociente

logb M/N = logb M - logb N

Dividir dos números con la misma base, restar los exponentes.

Ejemplo : log8 56 - log8 7 = log8(56/7)=log88 = 1

Regla de la potencia

Eleva una expresión exponencial a la potencia y multiplica los exponentes.

Logb Mp = P logb M

Ejemplo: log 1003 = 3. Log 100 = 3 x 2 = 6

Regla del exponente cero

loga 1 = 0.

Regla del cambio de base

logb (x) = ln x / ln b o logb (x) = log10 x / log10 b

Otras reglas importantes de la función logarítmica

Logb b = 1 Ejemplo : log1010 = 1

Logb bx = x Ejemplo : log10 10x = xb logbx=x. Sustituyendo y= logbx , se convierte en by = x

También hay algunas funciones logarítmicas con fracciones. Es útil encontrar el logaritmo de una fracción aplicando las identidades

ln(ab)= ln(a)+ln(b)
ln(ax) = x ln (a)

Vídeos de Funcion logaritmica